机器学习-支持向量机核函数

SVM回顾

上文支持向量机SVM ，简单总结了对于线性可分数据的SVM的算法原理，现在我们对于非线性可分以及有噪声存在的时候我们需要对基本SVM算法的改进进行下总结其中包括:

核函数在SVN算法中的使用
引入松弛变量和惩罚函数的软间隔分类器

我们再回顾一下我们上次推导最终的对偶优化问题，我们后面的改进和优化都是在对偶问题形式上展开的。

SVM标准形式

$min_{w,b}\frac{1}{2}{||w||}^2$

$s.t.y_i(w^Tx+b)\ge1, i=1,2,\cdot \cdot \cdot m$

对偶形式

$max_a \sum_{i=1}^na_i-\frac12\sum_{i=1,j=1}^na_ia_j{x_i}^Tx_jy_iy_j$

$s.t. ,a_i\ge0, i=1,\cdot \cdot \cdot n$

$\sum_{i=1}^na_iy_i=0$

SVM预测模型

SVM通过分割超平面$w^Tx+b$来获取未知数据的类型，将上述的$w和b$替换就可以得到：

$h_{w,b}(x)=g(w^Tx+b)=g(\sum_{i=1}^n a_iy_i{x_i}^Tx+b)$

通过$g(x)来输出+1还是-1$来获取未知数据的类型

核函数

前面我在推导SVM算法的时候解决的一般是线性可分的数据，而对于非线性可分的数据的时候（如图），我们就需要引出核函数

所以对于这类问题，SVM的处理方法就是选择一个核函数，其通过将数据映射到更高维的特征空间（非线性映射），使得样本在这个特征空间内线性可分，从而解决原始空间中线性不可分的问题。

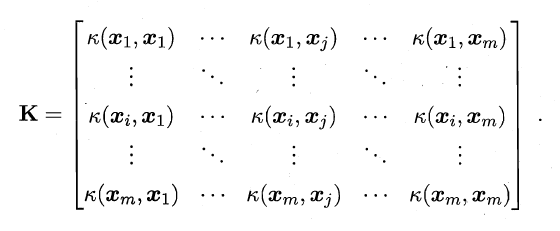
从数据上来看就是把数据映射到多维：例如从一维映射到四维：

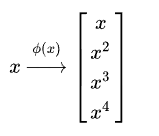
这里是通过$\Phi(x)$把数据映射到高维空间，所以对应的对偶问题就改写为：

$max_a \sum_{i=1}^na_i-\frac12\sum_{i=1,j=1}^na_ia_j{\Phi(x_i)}^T\Phi(x_j）y_iy_j$

$s.t. ,a_i\ge0, i=1,\cdot \cdot \cdot n$

$\sum_{i=1}^na_iy_i=0$

${\Phi(x_i)}^T\Phi(x_j$,是我们把样本$x_i和 x_j$映射到特征空间之后的内积，但是由于特征空间的维数可能很高，甚至是无穷维，所以直接计算${\Phi(x_i)}^T\Phi(x_j）$是非常困难的，但是我们有又必须要计算他，所以为了避开这个障碍，我们就设一个函数：

$k(x_i,x_j)={\Phi(x_i)}^T\Phi(x_j）$

我们就直接通过函数$h(\cdot, \cdot)$计算获得${\Phi(x_i)}^T\Phi(x_j）$的结果，就不必直接去计算高维甚至无穷维的特征空间中的内积。于是对偶问题和预测模型就改写为：

$max_a \sum_{i=1}^na_i-\frac12\sum_{i=1,j=1}^na_ia_jk(x_i,x_j)y_iy_j$

$s.t. ,a_i\ge0, i=1,\cdot \cdot \cdot n$

$\sum_{i=1}^na_iy_i=0$

$f(x)=\sum_{i=1}^n a_iy_i{x_i}^Tx+b=\sum_{i=1}^n a_iy_ik(x,x_i)+b$

而这里的$k(\cdot, \cdot )$就是核函数（kernel function）.上述的$f(x)$显示出模型最优解可通过训练样本的核函数展开，这也就是支持向量展式。

核函数定理

令$X$为输入空间，$k(\cdot , \cdot )$是定义在$X \times X$上的对称函数，则$k$是核函数当且仅当对于数据$D={x_1,x_2 ,\cdot \cdot \cdot x_n}$，“核矩阵”K就是总是一个半正定矩阵：

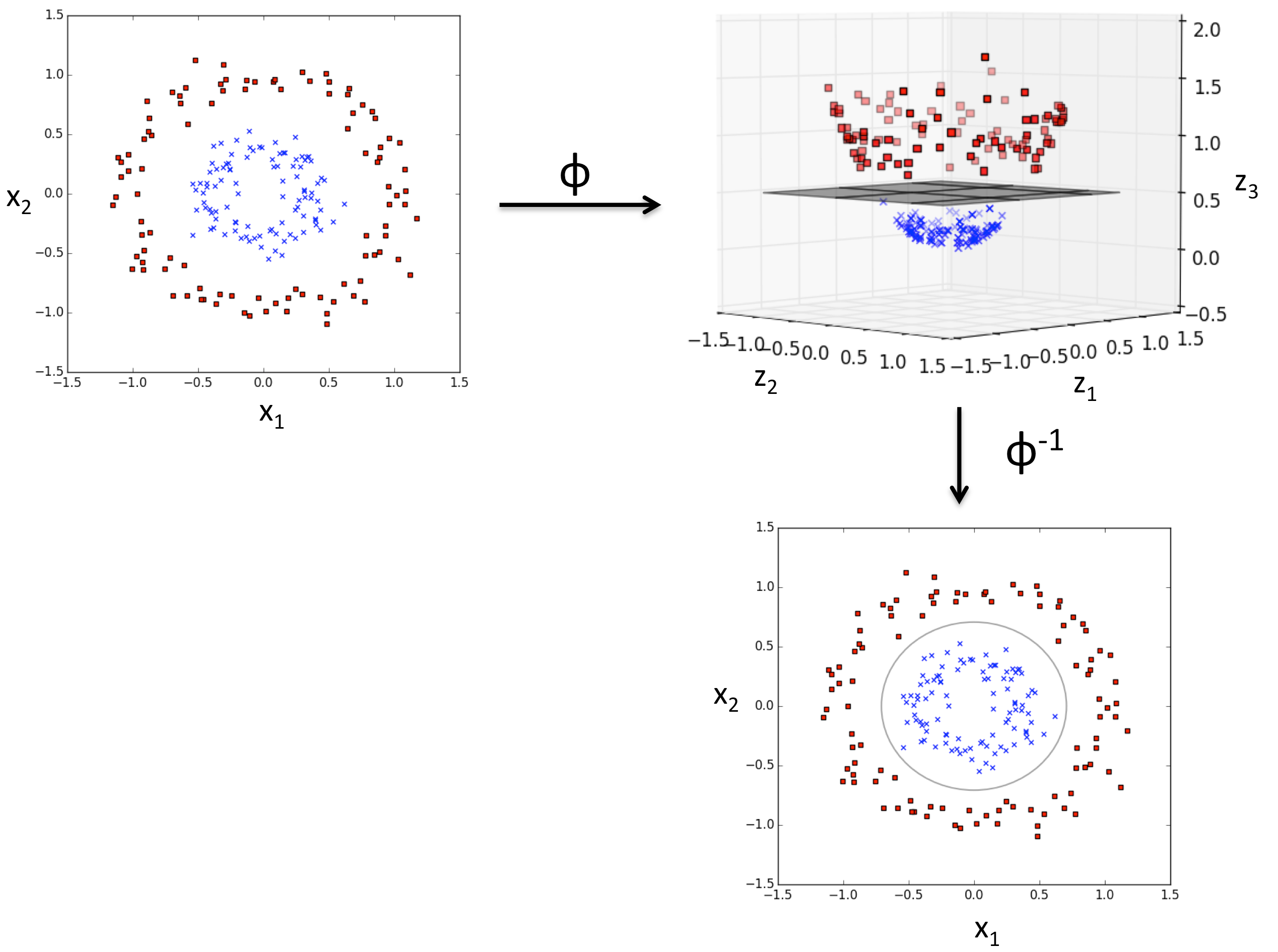
通俗来讲：只要一个对称函数所对应的核矩阵是半正定矩阵，它就能作为核函数。

常用的核函数

线性核：$k(x_i,x_j)={x_i}^Tx_j$
多项式核：$k(x_i,x_j)=({x_i}^Tx_j)^n, n\ge1$为多项式的次数
高斯核：$k(x_i,x_j)=e^{-\frac{||x_i-x_j||^2}{2\sigma^2}}, \sigma>0$为高斯核的带宽（width）
拉普拉斯核：$k(x_i,x_j)=e^{-\frac{||x_i-x_j||^2}{2\sigma}}, \sigma>0$
Sigmoid核：$k(x_i,x_j)=tanh(\beta{x_i}^Tx_j+\theta) $，$tanh为双曲正切函数，$$\beta>0, \theta>0$

通过函数组合：

若$k_1$和$k_2$为核函数，则对任意正数$\lambda_1, \lambda_2$，其线性组合：$\lambda_1k_1+\lambda_2k_2$
若$k_1$和$k_2$为核函数，则核函数的直积：$k_1 \otimes k_2 (x,z)=k_1(x,z)k_2(x,z)$
若$k_1$为核函数，则对于任意函数$g(x)$ :$k(x,z)=g(x)k_1(x,z)g(z)$

SVM回顾

SVM标准形式

$min_{w,b}\frac{1}{2}{||w||}^2$

$s.t.y_i(w^Tx+b)\ge1, i=1,2,\cdot \cdot \cdot m$

对偶形式

$max_a \sum_{i=1}^na_i-\frac12\sum_{i=1,j=1}^na_ia_j{x_i}^Tx_jy_iy_j$

$s.t. ,a_i\ge0, i=1,\cdot \cdot \cdot n$

$\sum_{i=1}^na_iy_i=0$

SVM预测模型

$h_{w,b}(x)=g(w^Tx+b)=g(\sum_{i=1}^n a_iy_i{x_i}^Tx+b)$

核函数

$max_a \sum_{i=1}^na_i-\frac12\sum_{i=1,j=1}^na_ia_j{\Phi(x_i)}^T\Phi(x_j）y_iy_j$

$s.t. ,a_i\ge0, i=1,\cdot \cdot \cdot n$

$\sum_{i=1}^na_iy_i=0$

$k(x_i,x_j)={\Phi(x_i)}^T\Phi(x_j）$

$max_a \sum_{i=1}^na_i-\frac12\sum_{i=1,j=1}^na_ia_jk(x_i,x_j)y_iy_j$

$s.t. ,a_i\ge0, i=1,\cdot \cdot \cdot n$

$\sum_{i=1}^na_iy_i=0$

$f(x)=\sum_{i=1}^n a_iy_i{x_i}^Tx+b=\sum_{i=1}^n a_iy_ik(x,x_i)+b$

核函数定理

常用的核函数

线性核：$k(x_i,x_j)={x_i}^Tx_j$

多项式核：$k(x_i,x_j)=({x_i}^Tx_j)^n, n\ge1$为多项式的次数

高斯核：$k(x_i,x_j)=e^{-\frac{||x_i-x_j||^2}{2\sigma^2}}, \sigma>0$为高斯核的带宽（width）

拉普拉斯核：$k(x_i,x_j)=e^{-\frac{||x_i-x_j||^2}{2\sigma}}, \sigma>0$

Sigmoid核：$k(x_i,x_j)=tanh(\beta{x_i}^Tx_j+\theta) $，$tanh为双曲正切函数，$$\beta>0, \theta>0$

通过函数组合：

若$k_1$和$k_2$为核函数，则对任意正数$\lambda_1, \lambda_2$，其线性组合：$\lambda_1k_1+\lambda_2k_2$

若$k_1$和$k_2$为核函数，则核函数的直积：$k_1 \otimes k_2 (x,z)=k_1(x,z)k_2(x,z)$

若$k_1$为核函数，则对于任意函数$g(x)$ :$k(x,z)=g(x)k_1(x,z)g(z)$