本文最后更新于:14 天前
支持向量机SVM的概念及起源
什么是支持向量机SVM
支持向量机,因其英文名为support vector machine,故一般简称SVM,通俗来讲,它是一种二类分类模型,其基本模型定义为特征空间上的间隔最大的线性分类器,其学习策略便是间隔最大化,最终可转化为一个凸二次规划问题的求解。
分类标准的起源:Logistic回归
我们先看看什么是线性分类器
给定一些数据点,它们分别属于两个不同的类,现在要找到一个线性分类器把这些数据分成两类。如果用$x$表示数据点,用$y$表示类别($y=1$或者$y=-1$,分别代表两个不同的类),一个线性分类器的学习目标便是要在$n$维的数据空间中找到一个超平面(hyper plane),这个超平面的方程可以表示为($w^T$中的T代表转置):
$w^Tx+b=0$
Logistic回归目的是从特征学习出一个0/1分类模型,而这个模型是将特性的线性组合作为自变量,由于自变量的取值范围是负无穷到正无穷。因此,使用logistic函数(或称作sigmoid函数)将自变量映射到(0,1)上,映射后的值被认为是属于$y=1$的概率。
根据我们前面Logistic回归的推导 ,假设函数:
$h_\theta(x)=g(\theta^Tx)=\frac1{1+e^{-\theta^Tx}}$
其中x是n维特征向量,函数g就是Logistic函数。
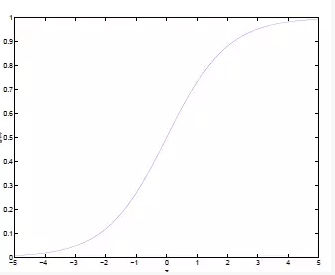
同样$g(z)=\frac{1}{1+e^{-z}}$的图像:

从图像中,我们就可以看出将无穷映射到了(0,1)。
而假设函数就是特征属于y=1的概率。
$P(y=1|x;\theta)=h_\theta(x) \\ P(y=0|x;\theta)=1-h_\theta(x)$
所以,我们在判别一个新的特征属于哪个类别的时候,就只需要求$h_\theta(x)$就可以了,由上面的图中可以看出如果$h_\theta(x)$ 大于0.5就是y=1的类,否则就是属于y=1的类。
然后我们尝试给Logistic回归做一个变形。首先,将使用的结果标签y=0和y=1替换为$y=-1,y=1 $,然后把$\theta_0$替换成b,把$w$替换$\theta_i$,所以就变换为:
$h_\theta(x)=g(w^Tx+b)$
所以我们就可以假设函数:$h_{w,b}(x)=g(w^Tx+b)$,中的g(z)做一个简化,将其简单映射到y=-1和y=1上。映射关系如下:
$ g(z)=\left\lbrace \begin{aligned} 1 && z \ge0 \\ -1 && z<0 \end{aligned} \right. $
然后我们举个线性分类的例子来看看
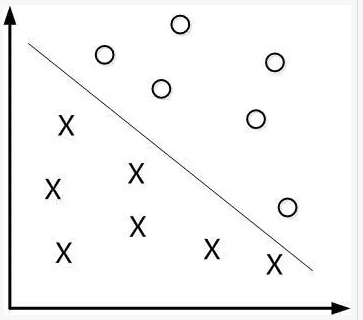
如下图所示,现在有一个二维平面,平面上有两种不同的数据,分别用圈和叉表示。由于这些数据是线性可分的,所以可以用一条直线将这两类数据分开,这条直线就相当于一个超平面,超平面一边的数据点所对应的y全是-1,另一边所对应的y全是1。
这个超平面可以用分类函数$f(x)=w^Tx+b$来表示,当f(x)等于0时候,x便是位于超平面上的点,而f(x)大于0的点对应y=1的数据点,f(x)小于0的点对应y=-1的点,如下图所示:
接下来的问题是,如何确定这个超平面呢?从直观上而言,这个超平面应该是最适合分开两类数据的直线。而判定“最适合”的标准就是这条直线离直线两边的数据的间隔最大。所以,得寻找有着最大间隔的超平面。
间隔与支持向量
SVM支持向量机(英文全称:support vector machine)是一个分类算法, 通过找到一个分类平面, 将数据分隔在平面两侧, 从而达到分类的目的。如下图所示, 直线表示的是训练出的一个分类平面, 将数据有效的分隔开。
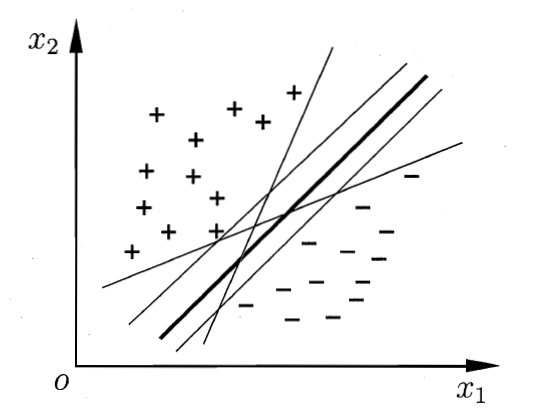
根据上面的逻辑,我们在做数据分隔的时候,有很多个分类平面,这时我们就需要找出“最优”的那一个平面模型,根据【超平面】【数据点】【分开】这几个词,我们可以想到最优的模型必然是最大程度地将数据点划分开的模型,不能靠近负样本也不能靠近正样本,要不偏不倚,并且与所有Support Vector的距离尽量大才可以。
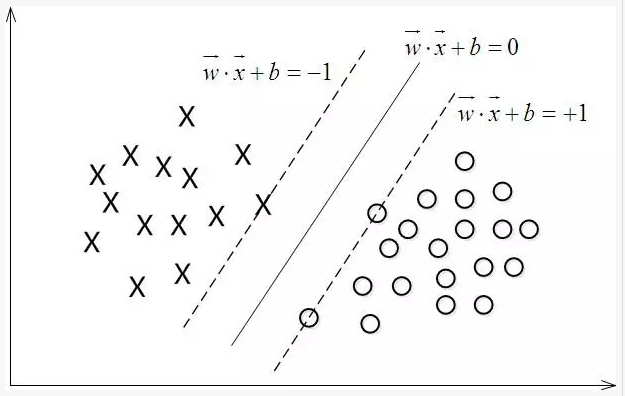
上图中 $x_0$ 是 $x $在超平面上的投影,$ω$是超平面的法向量.
超平面用线性方程来描述:
$w^T+b=0$
函数间隔
在超平面$w ^T x + b = 0$确定的情况下,$|w^Tx+b|$表示点距离超平面的距离,而超平面作为二分类器,如果$w^Tx+b>0$, 判断类别y为1, 否则判定为-1。从而引出函数间隔的定义:
$r=y(w^Tx+b)=yf(x)$
其中y是训练数据的类标记值, 如果$y(w^T x + b) >0$说明,预测的值和标记的值相同, 分类正确,而且值越大,说明点离平面越远,分类的可靠程度更高。这是对单个样本的函数定义, 对整个样本集来说,要找到所有样本中间隔值最小的作为整个集合的函数间隔:
$r=min \ r_i , i=1,2 \cdot \cdot \cdot n$
即w和b同时缩小或放大M倍后,超平面并没有变化,但是函数间隔跟着w和b变化。所以,需要加入约束条件使得函数间隔固定, 也就是几何间隔。
几何间隔
样本空间$x$到超平面$x_0$的距离:
$r=\frac{|w^Tx+b|}{||w||}$
如果超平面将样本成功分类,若$y_i=+1$,则有$w^Tx+b>0$;若$y_i=-1$,则有$w^Tx+b<0$;则下式成立
$ \left \lbrace \begin{aligned} w^Tx+b \ge+1&& y_i=+1 \\ w^Tx+b\le-1 && y_i=-1 \end{aligned} \right.$
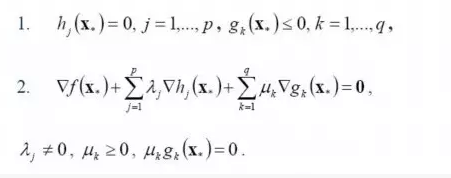
从上图中可以看出,距离超平面最近的这几个训练样本点使上述公式的等号成立,这几个训练样本就称为“支持向量”(support vector)
两个异类支持向量到超平面的距离之和(被称为间隔):
$r=\frac{2}{||w||}$
”最大间隔“的超平面
我们要找的”最大间隔“的超平面,即:
$max_{w,b}\frac{2}{||w||}$
$s.t.y_i(w^Tx+b)\ge1, i=1,2,\cdot \cdot \cdot m$
SVM的二次凸函数和约束条件
最大间隔分类器的求解, 可以转换为上面的一个最优化问题, 即在满足约束条件:
$y_i(w^Tx+b)\ge1, i=1,2,\cdot \cdot \cdot m$
求出就最大的$\frac1{||w||}$。
为更好的利用现有的理论和计算方法, 可以将求解$\frac1{||w||}$最大值, 转换为一个二次凸函数优化问题:求解 $min_{w,b}\frac{1}{2}{||w||}^2$, 两者问题是等价的。原来的问题转换为二次凸函数优化问题。在一定的约束条件下,目标最优,损失最小。
SVM的基本型
我们前面已经知道,最大化$||w||^{-1}$等价于最小化$||w||^2$,所以:
$min_{w,b}\frac{1}{2}{||w||}^2$
$s.t.y_i(w^Tx+b)\ge1, i=1,2,\cdot \cdot \cdot m$
拉格朗日构建方程
由于这个问题的特殊结构,还可以通过拉格朗日对偶性(Lagrange Duality)变换到对偶变量(dual variable)的优化问题,即通过求解与原问题等价的对偶问题(dual problem)得到原始问题的最优解,这就是线性可分条件下支持向量机的对偶算法.
这样做的优点在于:一者对偶问题往往更容易求解;二者可以自然的引入核函数,
进而推广到非线性分类问题。 具体来说就是对svm基本型的每条约束添加拉格朗日乘子$a_i\ge0$,则该问题的拉格朗日函数可写为:
$L(w,b,a)= \frac12 ||w||^2+\sum_{i=1}^na_i(1-y_i(w^Tx+b))$ $a_i=(a_1;a_2; \cdot \cdot \cdot a_m)$.
我们的目标是让拉格朗如函数$ L(ω,b,α)$ 针对 $α$ 达到最大值。为什么能够这么写呢,我们可以这样想,哪怕有一个 $y_i(ω^Tx_i+b)⩾1$不满足,只要让对应的 $α_i$ 是正无穷就好了。所以,如果$L(ω,b,α)$有有限的最大值,那么那些不等式条件是自然满足的。 之后,我们再让 $L(ω,b,α)$ 针对 $ω,b$ 达到最小值,就可以了。 从而,我们的目标函数变成:
原问题是极小极大的问题
$min_{w,b}max_aL(w,b,a)=p^*$
原始问题的对偶问题,是极大极小问题
$max_amin_{w,b}L(w,b,a)=b^*$
交换以后的新问题是原始问题的对偶问题,这个新问题的最优值用$d^*$来表示。而且有$d^∗⩽p^∗$,在满足某些条件的情况下,这两者相等,这个时候就可以通过求解对偶问题来间接地求解原始问题。
这所谓的“满足某些条件”就是要满足KKT条件。
$ \left\lbrace\ \begin{aligned} a_i \ge0 \\ y_i(w^Tx_i+b) -1\ge 0 \\ a_i(y_i(w^Tx_i+b)-1)=0 \end{aligned} \right. $
KKT条件的意义
一般地,一个最优化数学模型能够表示成下列标准形式:
$min.f(x)$
$s.t. h_j(x)=0,j=1,\cdot \cdot \cdot n$
$g_k(x)\le0,k=1,\cdot \cdot \cdot m$
$x\in X \subset R^n$
其中,f(x)是需要最小化的函数,h(x)是等式约束,g(x)是不等式约束,p和q分别为等式约束和不等式约束的数量。
凸优化的概念:$x\subset R^n$为一凸集,$f:x\to R$为一凸函数,凸优化就是要找出一点$x^\in X$,使得每一$x\in X$满足$f(x^)\le f(x)$
KKT条件的意义:它是一个非线性规划(Nonlinear Programming)问题能有最优化解法的必要和充分条件。
而KKT条件就是指上面最优化数学模型的标准形式中的最小点$ x*$ 必须满足下面的条件:

经过论证,我们这里的问题是满足KKT条件的(首先已经满足Slater condition,再者$f(x)$和$g(x)$也都是可微的,即$L$对$w$和$b$都可导),因此现在我们便转化为求解第二个问题。
也就是说,原始问题通过满足KKT条件,已经转化成了对偶问题。而求解这个对偶学习问题,分为3个步骤:首先要让$L(w,b,a)$关于$w$和$b$最小化,然后求对$a$的极大,最后利用SMO算法求解对偶问题中的拉格朗日乘子。
对偶问题求解
首先固定$a$,先求出$min_{w,b}L(w,b,a)$,所以分别对$w,b$进行求偏导并令其等于0。
$\frac{\partial L(w,b,a)}{\partial w}=\frac{\partial(\frac12w^Tw+\sum_{i=1}^na_i-\sum_{i=1}^n a_iby_i-\sum_{i=1}^n a_iy_iw^Tx)}{\partial w} =0$
$\frac{\partial L(w,b,a)}{\partial b}=\frac{\partial(\frac12w^Tw+\sum_{i=1}^na_i-\sum_{i=1}^n a_iby_i-\sum_{i=1}^n a_iy_iw^Tx)}{\partial b} =0$
$w=\sum_{i=1}^na_ix_iy_i$
$\sum_{i=1}^na_iy_i=0$
然后我们将以上结果带入原式$L(w,b,a)$:
$L(w,b,a)= \frac12 ||w||^2+\sum_{i=1}^na_i(1-y_i(w^Tx+b))$
$=\frac12w^Tw+\sum_{i=1}^na_i-\sum_{i=1}^n a_iby_i-\sum_{i=1}^n a_iy_iw^Tx$
导入$w=\sum_{i=1}^na_ix_iy_i$:
$=\frac12w^T(\sum_{i=1}^na_ix_iy_i)+\sum_{i=1}^na_i-\sum_{i=1}^n a_iby_i-w^T(\sum_{i=1}^n a_iy_ix)$
导入$\sum_{i=1}^na_iy_i=0$:
$=\sum_{i=1}^na_i-\frac12w^T(\sum_{i=1}^na_ix_iy_i)$
$=\sum_{i=1}^na_i-\frac12{(\sum_{i=1}^na_ix_iy_i)}^T(\sum_{i=1}^na_ix_iy_i)$
$=\sum_{i=1}^na_i-\frac12(\sum_{i=1}^na_i{x_i}^Ty_i)(\sum_{i=1}^na_ix_iy_i)$
$=\sum_{i=1}^na_i-\frac12\sum_{i=1,j=1}^na_ia_j{x_i}^Tx_jy_iy_j$
从上面的最后一个式子,我们可以看出,此时的拉格朗日函数只包含了一个变量,那就是$a_i$(求出了$a_i$便能求出$w,b$,然后我们的分类函数$f(x)=w^Tx+b$就非常容易的求出来了)。
然后求对$a$的极大值:
即是关于对偶问题的最优化问题。经过上面第一个步骤的求w和b,得到的拉格朗日函数式子已经没有了变量w,b,只有从上面的式子得到:
$max_a \sum_{i=1}^na_i-\frac12\sum_{i=1,j=1}^na_ia_j{x_i}^Tx_jy_iy_j$
$s.t. ,a_i\ge0, i=1,\cdot \cdot \cdot n$
$\sum_{i=1}^na_iy_i=0$
我们一般用SMO算法来求解$a$
SMO优化算法
SMO算法由Microsoft Research的John C. Platt在1998年提出,并成为最快的二次规划优化算法,特别针对线性SVM和数据稀疏时性能更优。
SMO的基本思路是先固定$a_i$之外的所有参数,然后求$a_i$上的极值。由于存在约束$\sum_{i=1}^na_iy_i=0$,若固定$a_i$之外的其他变量,则$a_i$可由其他变量导出。于是,SMO每次选择两个变量$a_i和a_j$,并固定其他参数。这样,在参数初始化后,SMO不断执行如下两个步骤直至收敛:
选取一对需更新的变量$a_i和 a_j$.
固定$a_i和 a_j$以外的参数,求解$max_a \sum_{i=1}^na_i-\frac12\sum_{i=1,j=1}^na_ia_j{x_i}^Tx_jy_iy_j$,获得更新后的$a_i和 a_j$
那如何做才能做到不断收敛呢?
注意只需选取的$a_i和 a_j$ 中有一个不满足KKT的条件,目标函数就会在不断迭代后减小。直观来说KKT条件的违背的程度越大,则变量更新后可能导致的目标函数值减幅越大,
那如何选取变量呢?
第一个变量SMO 先选取违背KKT条件程度最大的变量。
第二个变量应该选择一个使目标函数值减小最快的变量。
但是由于比较各变量所对应的目标函数值减幅的复杂度过高,因此SMO就采用了一个启发式:使选取的变量所对应的样本之间的间隔最大。
总结:这样选取的两个变量有很大的差别,与对两个相似的变量进行更新相比,对它们进行更新会带给目标函数值更大的变化。SMO之所以高效,就是在于固定其他参数后,只优化两个参数的过程能做到非常高效。
所以:只考虑$a_i和 a_j$时,约束条件就改变为:
$max_a \sum_{i=1}^na_i-\frac12\sum_{i=1,j=1}^na_ia_j{x_i}^Tx_jy_iy_j$
$s.t. ,a_iy_i+a_jy_j=c, a_i \ge 0, a_j \ge 0$
$\sum_{i=1}^na_iy_i=0$
其中:$c= -\sum_{k \ne i,j}a_ky_k$是使$\sum_{i=1}^na_iy_i=0$ 成立的常数。
然后用$a_iy_i+a_jy_j=c$ 消去变量$a_j$ ,就可以得到一个关于$a_j$ 的单变量的二次规划问题,通过约束条件$a_i \ge0$,就可以解出这个二次规划问题的闭式解,于是不必调用数值优化算法就可以很快的算出更新后的$a_i 和 a_j$。
线性模型
用SMO 解出$a$后,我们前面以前算出$w$的值,所以我们还需要在前面的基础上算出b的值
$w=\sum_{i=1}^na_ix_iy_i$
$b=y_j-\sum_{i=1}^n a_iy_i{x_i}^Tx_j$
所以就可以得到模型
$f(x)=w^Tx+b=\sum_{i=1}^n a_iy_i{x_i}^Tx+b$
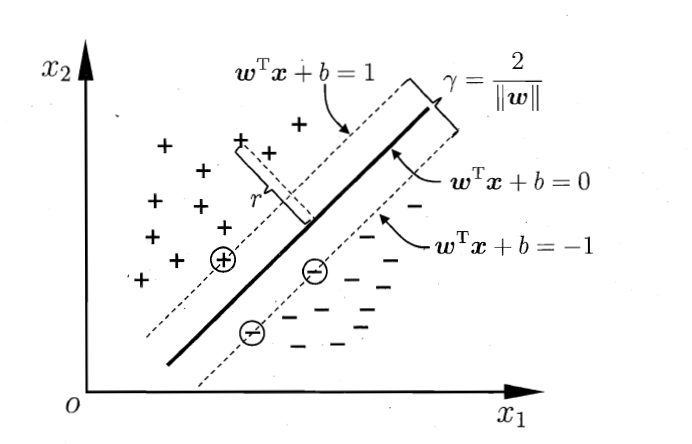
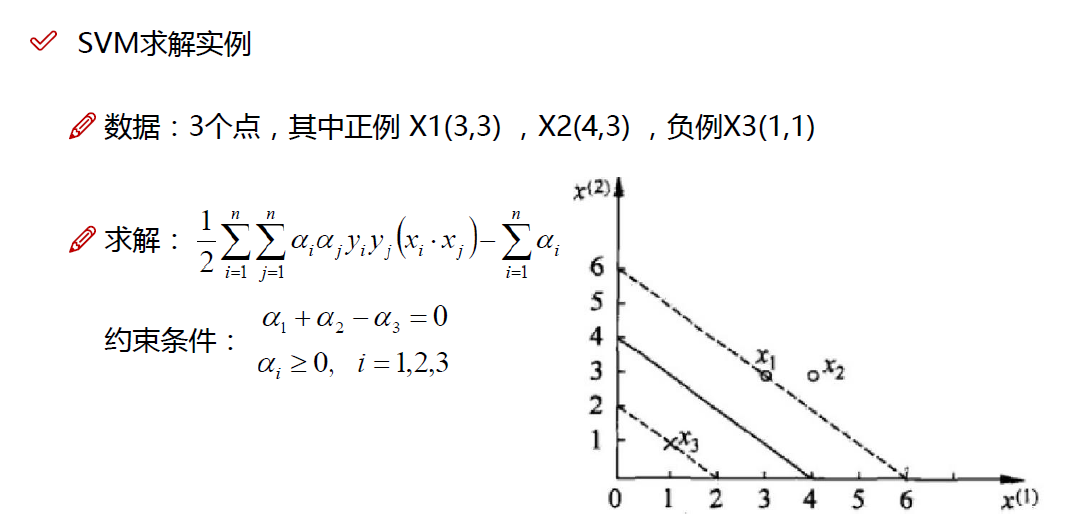
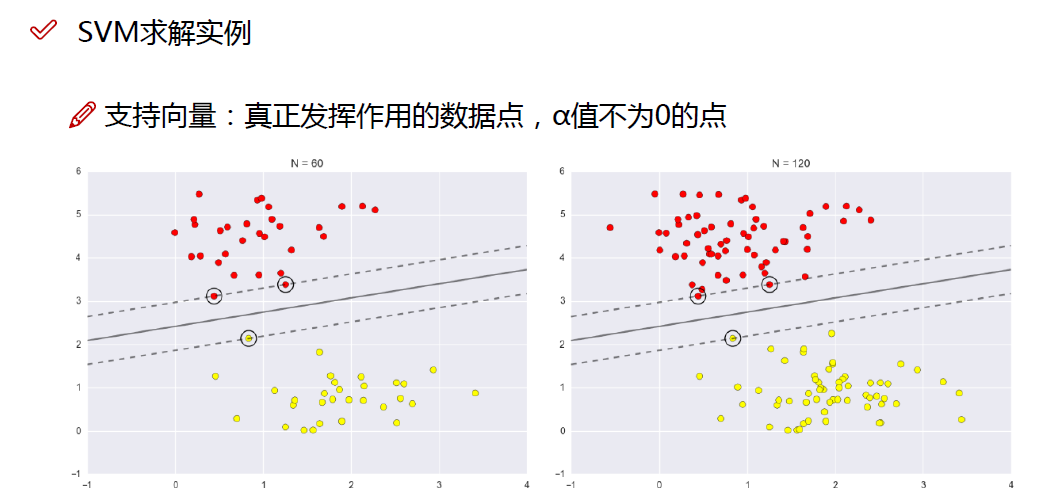
实战一下
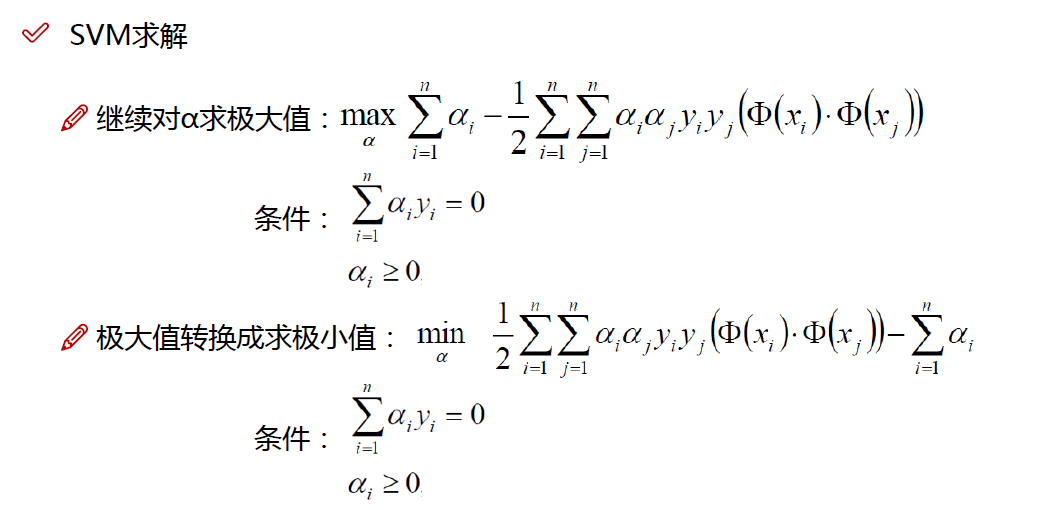

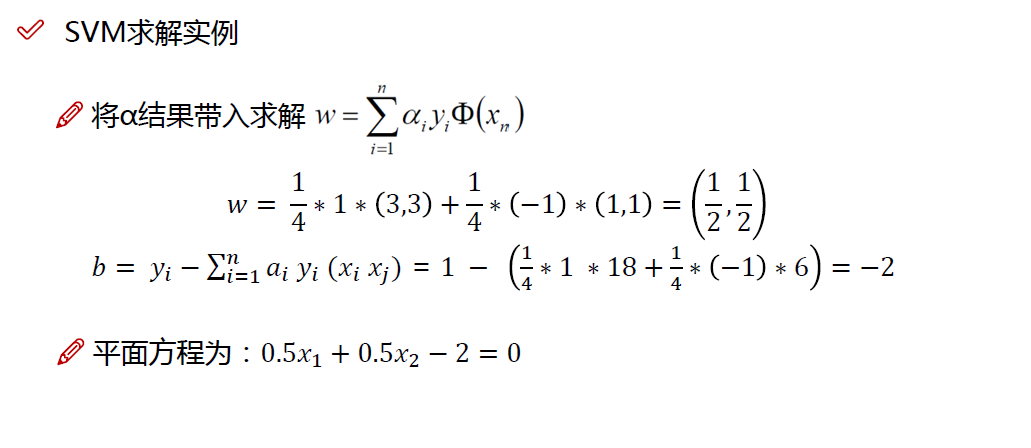
本博客所有文章除特别声明外,均采用 CC BY-SA 3.0协议 。转载请注明出处!