软间隔和正则化

我们在最开始讨论支持向量机的时候，我们就假定数据在样本空间是线性可分的，也就是我们可以找到一个可行的超平面将数据完全分开。后来为了处理非线性数据，我们又推出使用 Kernel 方法对原来的线性 SVM 进行了推广，使得非线性的的情况也能处理。虽然通过映射$\Phi(x)$将原始数据映射到高维空间之后，使得数据集在特征空间中线性可分，但是也很难断定这个貌似线性可分的结果是不是由于过拟合造成的。

软间隔的概念

为了缓解该问题，我们允许支持向量机在一些样本上出错。如图所示：

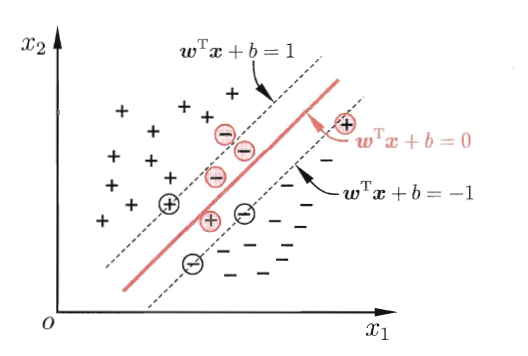
前面我们所介绍的支持向量机的形式是每个样本必须分正确，这是“硬间隔”，而软间隔就是允许一些样本不满足约束.

软间隔分类器

软间隔分类器(soft margin classifier)可以解决两种情况.

前面我们都假定数据是线性可分的, 但实际上数据即使映射到了高维也不一定是线性可分. 这个时候就要对超平面进行一个调整, 即这里所说的软间隔.

另一种情况是即使数据是线性可分的, 但数据中可能存在噪点. 而如果按照前面那种常规处理的话, 这些噪点会对我们的结果造成很大的影响.这个时候也是需要使用软间隔来尽可能减少噪点对我们的影响.

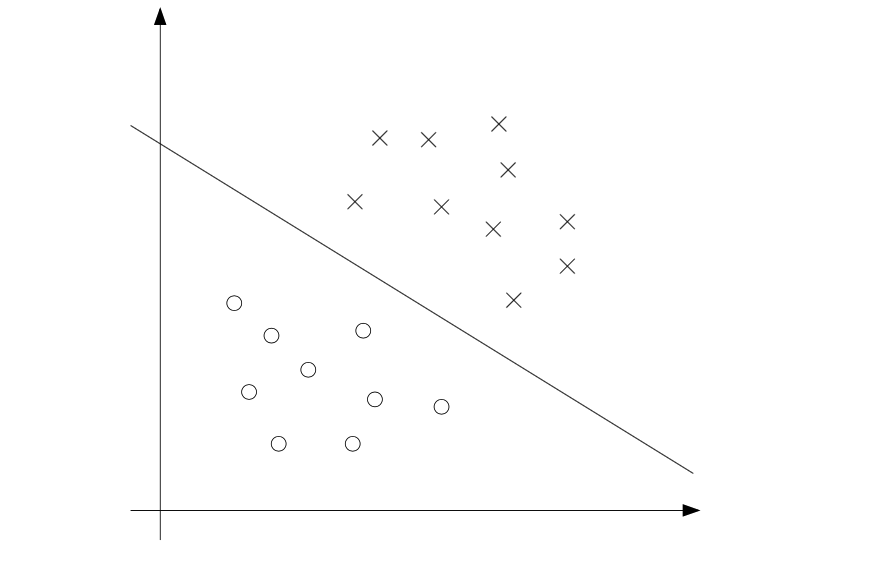
如下图所示, 如果数据是线性可分并且不存在噪点的话, 我们可以找到一个完美的分类超平面:

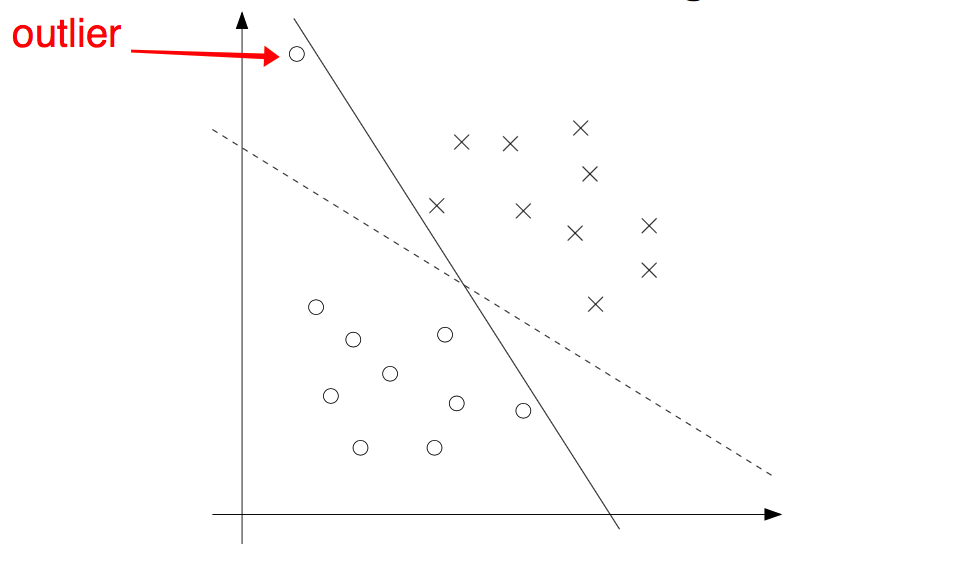
但是, 如果数据中出现了一个噪点并且仍然是线性可分, 如果我们还是按照之前的办法处理, 那么我们就会得到如下的分类超平面, 这明显是不合理的，这也就出现了过拟合的状况.

软间隔支持向量机：

在硬间隔最大化的目标函数中添加松弛变量和惩罚参数，在约束条件中添加松弛变量，即

$min_{w,b}\frac{1}{2}{||w||}^2+C\sum_{i=1}^n \xi_i$

$s.t.y_i(w^Tx+b)\ge1-\xi_i,\xi_i\ge0, i=1,2,\cdot \cdot \cdot m$

注意：

• 要使间隔尽量大，那$\frac{1}{2}{||w||}^2$尽量小

• 误分类点的个数尽量小，即松弛变量$\xi_i$尽量小，$C$为调和两者的系数

构建拉格朗日函数

在软间隔支持向量机中每个样本都有一个对应的松弛变量，用来表示该样本不满足约束条件:$y_i(w^Tx+b)\ge1$

但是这个函数同样是一个二次规划问题，我们就可以通过拉格朗日乘子法就可以得到拉格朗日函数。

$L(w,b,a,\xi,u)=\frac{1}{2}{||w||}^2+C\sum_{i=1}^n \xi_i+\sum_{i=1}^na_i(1-\xi_i- y_i(w^Tx+b))-\sum_{i=1}^nu_i\xi_i$

其中$a_i\ge0, u_i\ge0$是拉格朗日的乘子。

令$L(w,b,a,\xi,u)$对$w,b,\xi_i$的偏导为零可得：

求导方法就按照支持向量机的算法推导来进行：

$w=\sum_{i=1}^na_ix_iy_i$

$\sum_{i=1}^na_iy_i=0$

$C=a_i+u_i$

对偶问题

类似线性可分支持向量机中做法，引入拉格朗日乘子并构建拉格朗日函数，利用拉格朗日对偶性，问题转化为求解对偶问题

$max_a \sum_{i=1}^na_i-\frac12\sum_{i=1,j=1}^na_ia_j{x_i}^Tx_jy_iy_j$

$s.t. ,0\le a_i\le C, i=1,\cdot \cdot \cdot n$

$\sum_{i=1}^na_iy_i=0$

与前面所推导的硬间隔下的对偶问题，两者的差别就在于对偶变量的约束不同，前者是$0\le a_i$，后者是$0\le a_i\le C$。后续同样可以引入核函数得到对应的支持向量展开式。

软间隔支持向量机KKT条件

$ \left\lbrace\ \begin{aligned} a_i \ge0 , u_i\ge0\\ y_i(w^Tx_i+b) -1+\xi_i\ge 0 \\ a_i(y_i(w^Tx_i+b)-1+\xi_i)=0 \\ \xi_i\ge0, u_i\xi_i=0 \end{aligned} \right. $

合页损失函数

间隔/线性支持向量机的原始问题可以等价于添加了正则化项的合页损失函数，即最小化以下目标函数

$min_{w,b}\sum_{i=1}^n[1- y_i(w^Tx+b)]_++\lambda||w||^2$

• 第一项为合页损失函数 $L(y(w^Tx+b))=[1- y_i(w^Tx+b)]+$，我们再结合前面我在进行数据分割的约束条件，一般对于函数$[z]+$就有：

$[z]_+=z, 如果z>0$

$[z]_+=0, 如果z<0$

​ 这样原式就能表明当样本点$x_i,y_i$被正确分类且函数间隔$y_i(w^Tx+b)>1$时损失为0，

​ 否则损失就为$1-y_i(w^Tx+b)$

• 第二项为正则化项，是系数为λ的w的L2范数

线性支持向量机的原始最优化问题与上述目标函数的最优化问题是等价的

我们把一些损失函数做一个对比：

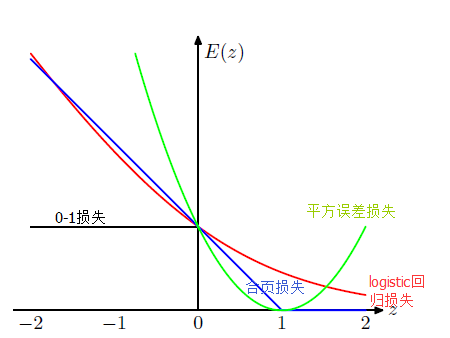
如图所示为常用的一些损失函数，可以看到，各个图中损失函数的曲线基本位于0-1损失函数的上方，所以可以作为0-1损失函数的上界；

• 由于0-1损失函数不是连续可导的，直接优化由其构成的目标损失函数比较困难，所以对于svm而言，可以认为是在优化由0-1损失函数的上界(合页损失函数)构成的目标函数，又称为代理损失函数

• 合页损失函数对学习有更高的要求

常用替代损失函数

通常具有较好的数学性质，比如凸的连续函数且是0/1损失函数的上界

• hinge损失 ： $l_{hinge}(z)=max(0,1-z)$

• 指数损失： $l_{exp}(z)=exp(-z)$

• 对率损失： $l_{log}(z)=log(1+exp(-z))$

SVM和Logistic Regression对比

相同点：优化目标相近，通常情形下性能也相当

不同点：

• LR的优势在于其输出具有自然的概率意义，给出预测标记的同时也给出了概率，而SVM要想得到概率输出需特殊处理
• LR能直接用于多分类任务，而SVM则需要进行推广
• SVM的解具有稀疏性（仅依赖于支持向量），LR对应的对率损失则是光滑的单调递减函数，因此LR的解依赖于更多的训练样本，其预测开销更大