相对位姿测量算法

【基于空间多点】

• 相对位姿估计的基本问题

  • 已知：相机内参数；多个空间上的特征点(非共面)在目标坐标系(3D)和相平面坐标系(2D)坐标。
  • 输出：目标坐标系相对相机坐标系的位置和姿态。

  

• 基本思想示意

  

• 线性求解

  • 对每一个特征点，均有：

    

  • 对每一个特征点，均有：

    

  • 展开第一行

    

  • 类似展开第二、第三行：

    

  • 消去$Z_c$

    

  • 上二式右侧分母移到左边，得：

    

  • 整理为矩阵形式

    

  • 对于每一个点都可以形成如上两个方程，对于多个点，可进行堆叠，并记成矩阵形式：

    

  • 有六个或以上特征点且非共面时，可求解：

    

  • 上面求出的只有11个参数，且多一个/t3. 最后一个变量可利用如下约束求出

    

  • 线性求解总结

    利用矩阵的QR分解，得到最终的旋转矩阵非奇异矩阵P的正交三角分解：P=QR, 其中Q(维数n*s): 正交阵； R :上三角阵

    证明思路：对P 中各向量进行正交化

    

【扩展】

• 根据旋转矩阵计算旋转角

  相机坐标系想要转到与世界坐标系完全平行（即坐标轴完全平行，且方向相同），需要旋转3次，设原始相机坐标系为C0
  1、 C0绕其Z轴旋转，得到新的坐标系C1；
  2、 C1绕其Y轴旋转，得到新的坐标系C2（注意旋转轴为C1的Y轴，而非C0的Y轴）；
  3、 C2绕其X轴旋转，得到新的坐标系C3。此时C3与世界坐标系完全平行。

  

• Rodrigues旋转

  

• 空间的任何一个旋转，可表达为一个向量绕旋转轴旋转给定角度。可用四元数表达：

  

• 

• 

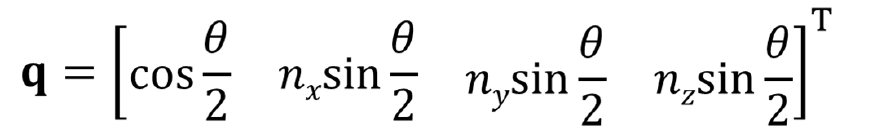
【基于平面多特征点】

• 基本问题

  已知：相机内参数；多个平面上的特征点在目标坐标系(3D)和相平面坐标系(2D)坐标。

  输出：目标坐标系相对相机坐标系的位置和姿态。

• 平面特征点相对位姿估计——线性求解

  • 设$Z_t=0$(特征共面), 则对每一个特征点，均有：

    

  • 得到两个方程

    

  • 未知数线性求解

    

  • 对于每一个点都可以形成如上两个方程，对于>=4个点，可使用类似PnP方法求得解：

    

【总结】

• 在已知至少六个空间点三维点坐标的条件下，可通过点的图像坐标及相对位姿估计算法计算相对位姿。
• 在已知至少四个平面点三维点坐标的条件下，可通过点的图像坐标及相对位姿估计算法计算相对位姿。

代码演示

#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time    : 2019/2/26 21:25
# @Author  : Seven
# @File    : PositionMeasurement.py
# @Software: PyCharm
# function : 实现位姿测量算法
import cv2
import numpy as np
import glob

# 加载相机标定的数据
with np.load('C.npz') as X:
    mtx, dist, _, _ = [X[i] for i in ('mtx', 'dist', 'rvecs', 'tvecs')]


def draw(img, corners, imgpts):
    """
    在图片上画出三维坐标轴
    :param img: 图片原数据
    :param corners: 图像平面点坐标点
    :param imgpts: 三维点投影到二维图像平面上的坐标
    :return:
    """
    corner = tuple(corners[0].ravel())
    cv2.line(img, corner, tuple(imgpts[0].ravel()), (255, 0, 0), 5)
    cv2.line(img, corner, tuple(imgpts[1].ravel()), (0, 255, 0), 5)
    cv2.line(img, corner, tuple(imgpts[2].ravel()), (0, 0, 255), 5)
    return img


# 初始化目标坐标系的3D点
objp = np.zeros((6 * 7, 3), np.float32)
objp[:, :2] = np.mgrid[0:7, 0:6].T.reshape(-1, 2)
# 初始化三维坐标系
axis = np.float32([[3, 0, 0], [0, 3, 0], [0, 0, -3]]).reshape(-1, 3)  # 坐标轴
# 加载打包所有图片数据
images = glob.glob('image/*.jpg')
for fname in images:
    img = cv2.imread(fname)
    gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
    # 找到图像平面点坐标点
    ret, corners = cv2.findChessboardCorners(gray, (7, 6), None)
    if ret:
        # PnP计算得出旋转向量和平移向量
        _, rvecs, tvecs, _ = cv2.solvePnPRansac(objp, corners, mtx, dist)
        print("旋转变量", rvecs)
        print("平移变量", tvecs)
        # 计算三维点投影到二维图像平面上的坐标
        imgpts, jac = cv2.projectPoints(axis, rvecs, tvecs, mtx, dist)
        # 把坐标显示图片上
        img = draw(img, corners, imgpts)
        cv2.imshow('img', img)
        cv2.waitKey(500)

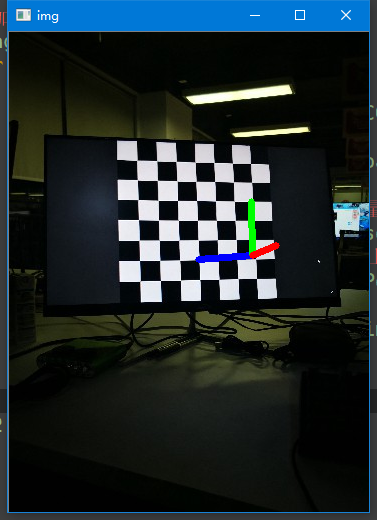
cv2.destroyAllWindows()

运行结果