本文最后更新于:14 天前
图像滤波基本原理
图像信息在采集过程中往往受到各种噪声源的干扰,这些噪声在图像上的常常表现为一些孤立像素点,这可理解为像素的灰度是空间相关的,即噪声点像素灰度与它们临近像素的灰度有着显著不同。通常,一般的前置图像处理后的信息仍然带有后续所不希望夹带的孤立像素点,这种干扰或孤立像素点如不经过滤波处理,会对以后的图像区域分割、分析和判断带来影响。
基本图像预处理滤波方法
图像滤波与卷积
【公式定义】
与1维信号滤波类似,图像滤波由卷积定义。

在图像中, 以模板形式定义。

注意:如果滤波器是对称的,那么两个公式就是等价的。
$f(x, y)$为图片原始数据、$g(x, y)$为卷积核。
【计算方式】
举个栗子:
假设一张图像有 5x5 个像素,1 代表白,0 代表黑,这幅图像被视为 5x5 的单色图像。现在用一个由随机地 0 和 1 组成的 3x3 矩阵去和图像中的子区域做Hadamard乘积,每次迭代移动一个像素,这样该乘法会得到一个新的 3x3 的矩阵。下面的动图展示了这个过程。

直观上来理解:
- 用一个小的权重矩阵去覆盖输入数据,对应位置元素加权相乘,其和作为结果的一个像素点。
- 这个权重在输入数据上滑动,形成一张新的矩阵
- 这个权重矩阵就被称为
卷积核(convolution kernel) - 其覆盖的位置称为
感受野(receptive fileld ) - 生成的新矩阵叫做
特征图(feature map)
分解开来,就如下图所示:
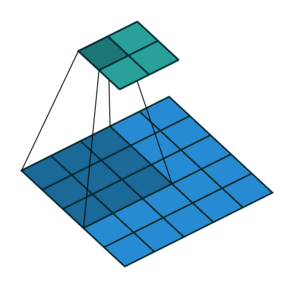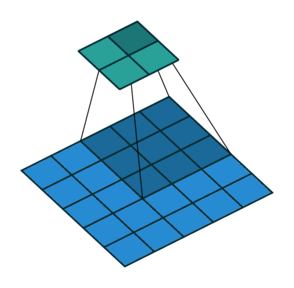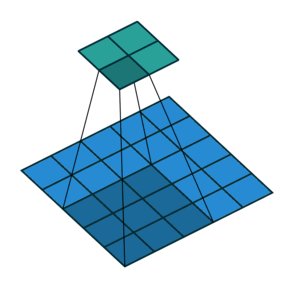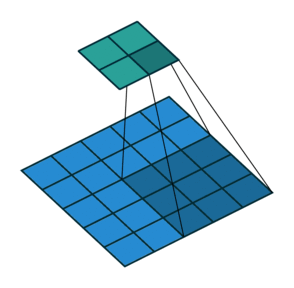
其中:
滑动的像素数量就叫做
步长(stride),步长为1,表示跳过1个像素,步长为2,就表示跳过2个像素,以此类推
以卷积核的边还是中心点作为开始/结束的依据,决定了卷积的
补齐(padding)方式。前面我们所举的栗子是valid方式,而same方式则会在图像的边缘用0补齐,如将前面的valid改为same方式,如图所示:

其采样方式对应变换为:

- 我们前面所提到的输入图像都是灰色的,只有一个通道,但是我们一般会遇到输入通道不只有一个,那么卷积核是三阶的,也就是说所有的通道的结果做累加。



当然,最后,这里有一个术语:“偏置(bias)”,每个输出滤波器都有一个偏置项,偏置被添加到输出通道产生最终输出通道。

图像去噪
【平均滤波】
在一个小区域内(通常是3*3)像素值平均。
数学公式定义
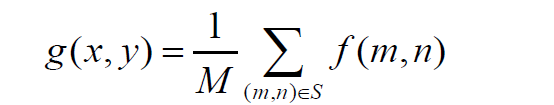
说明:如果在3*3的一个区域内,如果存在5个有效像素值,那么整体就除以5,以此类推。

【加权平均滤波】
在一个小区域内(通常是3*3)像素值加权平均。
数学公式定义

在进行基本平均滤波前,先把原始数据乘以一个指定的权重值,然后再进行平均。
普通卷积核
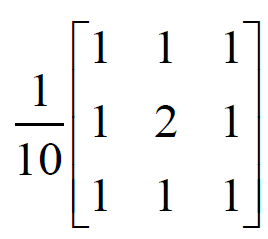
高斯卷积核

权重的分布符合高斯分布,所以叫高斯卷积核。
【中值滤波】
- 将滤波模板(含有若干个点的滑动窗口)在图像中漫游,并将模板中心与图中某个像素位置重合
- 读取模板中各对应像素的灰度值;
- 将这些灰度值从小到大排列;
- 取这一列数据的中间数据,将其赋给对应模板中心位置的像素。如果窗口中有奇数个元素,中值取元素按灰度值大小排序后的中间元素灰度值。如果窗口中有偶数个元素,中值取元素按灰度值大小排序后,中间两个元素灰度的平均值。因为图像为二维信号,中值滤波的窗口形状和尺寸对滤波器效果影响很大,不同图像内容和不同应用要求往往选用不同的窗口形状和尺寸。
示例
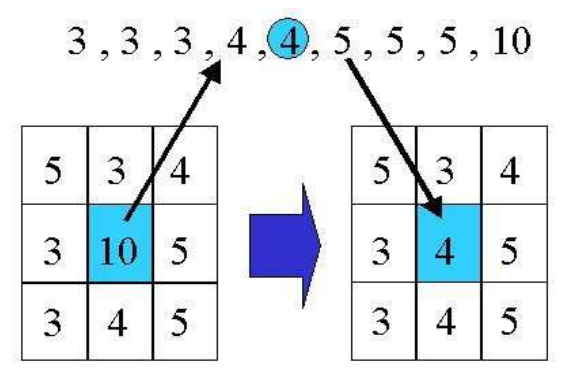
常用选取形式
3*3

5*5

中值滤波对椒盐噪声有效。
数学形态学滤波
【概述】
形态学(morphology)一词通常表示生物学的一个分支,该分支主要研究动植物的形态和结构。而我们图像处理中指的形态学,往往表示的是数学形态学。
数学形态学(Mathematical morphology) 是一门建立在格论和拓扑学基础之上的图像分析学科,是数学形态学图像处理的基本理论。其基本的运算包括:二值腐蚀和膨胀、二值开闭运算、骨架抽取、极限腐蚀、击中击不中变换、形态学梯度、Top-hat变换、颗粒分析、流域变换、灰值腐蚀和膨胀、灰值开闭运算、灰值形态学梯度等。
【膨胀和腐蚀】
按数学方面来说,膨胀或者腐蚀操作就是将图像(或图像的一部分区域,我们称之为A)与核(我们称之为B)进行卷积。
核可以是任何的形状和大小,它拥有一个单独定义出来的参考点,我们称其为锚点(anchorpoint)。多数情况下,核是一个小的中间带有参考点和实心正方形或者圆盘,其实,我们可以把核视为模板或者掩码。
膨胀
膨胀就是求局部最大值的操作,核B与图形卷积,即计算核B覆盖的区域的像素点的最大值,并把这个最大值赋值给参考点指定的像素。这样就会使图像中的高亮区域逐渐增长。
数学定义
$A\oplus B$表示集合A用
结构元素B膨胀。
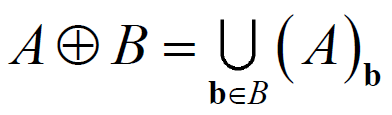
示例

腐蚀
腐蚀就是膨胀的相反操作,腐蚀就是求局部最小值的操作。
数学定义
$A\ominus B$表示集合A用
结构元素B腐蚀。
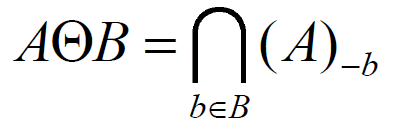
示例

【开闭运算】
膨胀和腐蚀并不互为逆运算,二者级联使用可生成新的形态学运算。
开运算
先腐蚀后膨胀
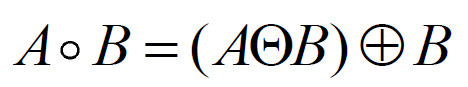
闭运算
先膨胀后腐蚀
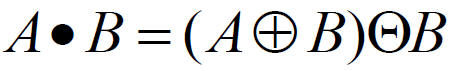
先开后闭
可有效的去除噪声。
滤波总结
- 滤波即卷积,由逐点乘积后累加得到
- 平滑滤波包括平均滤波、高斯滤波、中值滤波等方法,其中高斯滤波最为常用
- 数学形态学滤波基于腐蚀与膨胀两个基本操作
代码演示
import cv2
# 加载图片
image = cv2.imread('lena.jpg')
img = cv2.pyrDown(image)
cv2.imshow("source image", img)
# 高斯平滑滤波
gaussImage = cv2.GaussianBlur(img, (5, 5), 0)
cv2.imshow("gauss image", gaussImage)
# 中值滤波
medianImage = cv2.medianBlur(img, 5)
cv2.imshow("median image", medianImage)
# 形态学滤波
kernel = cv2.getStructuringElement(cv2.MORPH_RECT, (5, 5))
# 腐蚀图像
eroded = cv2.erode(img, kernel)
cv2.imshow("Eroded Image", eroded)
# 膨胀图像
dilated = cv2.dilate(img, kernel)
cv2.imshow("dilated Image", dilated)
# 形态学滤波-开运算
morphImage_open = cv2.morphologyEx(img, cv2.MORPH_OPEN, kernel)
cv2.imshow("image-open", morphImage_open)
# 形态学滤波-闭运算
morphImage_close = cv2.morphologyEx(img, cv2.MORPH_CLOSE, kernel)
cv2.imshow("image-close", morphImage_close)
# 形态学滤波-先开后闭运算
morphImage_open_close = cv2.morphologyEx(morphImage_open, cv2.MORPH_CLOSE, kernel)
cv2.imshow("image-open-close", morphImage_open_close)
cv2.waitKey(0)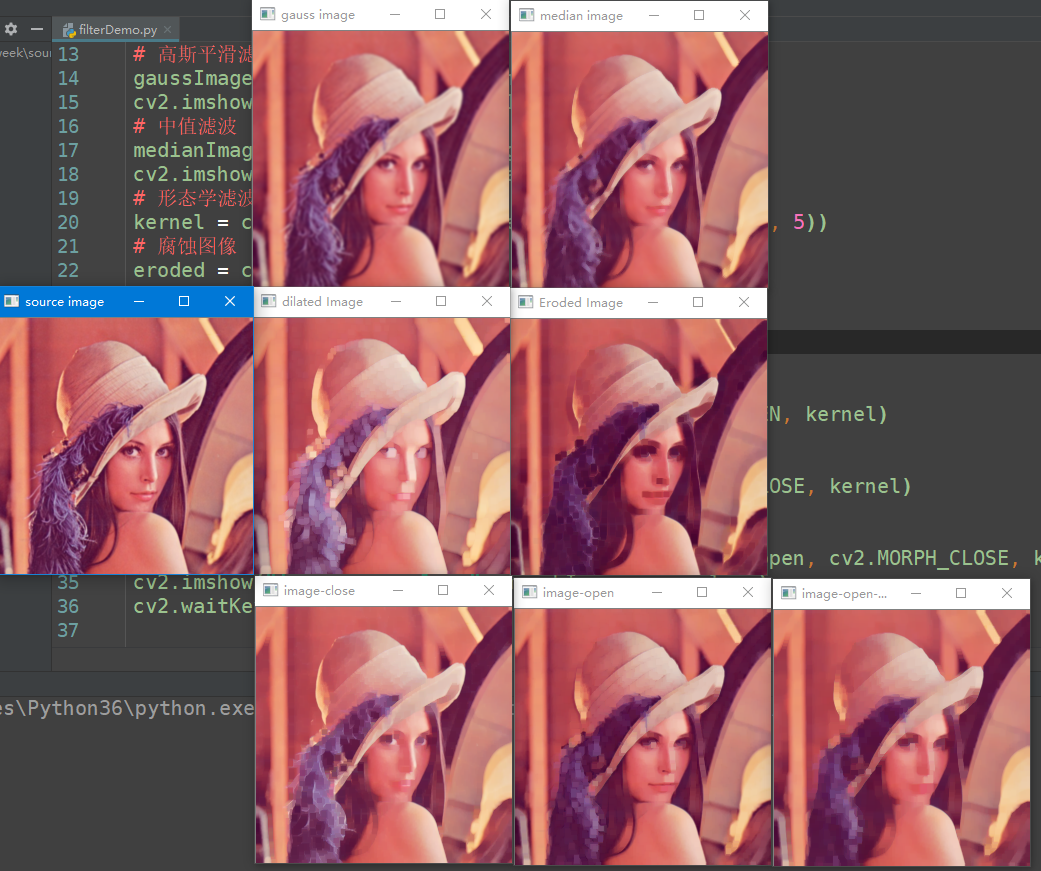
本博客所有文章除特别声明外,均采用 CC BY-SA 3.0协议 。转载请注明出处!