基本思想

边缘检测的基本思想是通过检测每个像素和其邻域的状态，以决定该像素是否位于一个物体的边界上。如果一个像素位于一个物体的边界上，则其邻域像素的灰度值的变化就比较大。假如可以应用某种算法检测出这种变化并进行量化表示，那么就可以确定物体的边界。

• 边缘检测的实质是微分。
• 实际中常用差分， X方向、Y方向。

基本算子

【Robert算子：一阶微分算子】

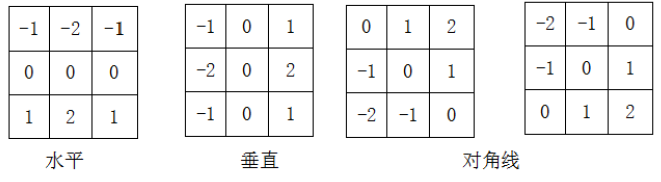
对于图像来说，是一个二维的离散型数集，通过推广二维连续型求函数偏导的方法，来求得图像的偏导数，即在(x,y)处的最大变化率，也就是这里的梯度：

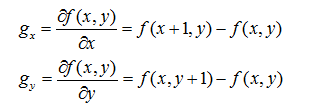
梯度是一个矢量，则(x,y)处的梯度表示为：

其大小为：

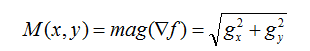
因为平方和平方根需要大量的计算开销，所以使用绝对值来近似梯度幅值：

方向与α(x,y)正交：

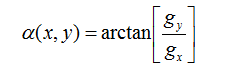
其对应的模板为：

图像的垂直和水平梯度

我们有时候也需要对角线方向的梯度，定义如下：

对应模板为：

Roberts 交叉梯度算子。

模板推导

垂直或水平算子模板

交叉算子模板

2*2 大小的模板在概念上很简单，但是他们对于用关于中心点对称的模板来计算边缘方向不是很有用，其最小模板大小为3*3。3*3 模板考虑了中心点对段数据的性质，并携带有关于边缘方向的更多信息。

【Prewitt算子：一阶微分算子】

prewitt算子一般使用的是3*3的模板

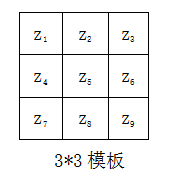
我如下定义水平、垂直和两对角线方向的梯度:

Prewitt算子：

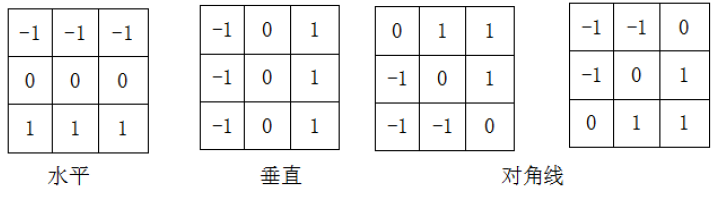
数学推导：

Prewitt 算子是由两部分组成，检测水平边缘的模板和检测垂直边缘的模板， Prewitt 算子一个方向求微分，一个方向求平均，所以对噪声相对不敏感。

【Sobel算子：一阶微分算子】

Sobel 算子是在Prewitt算子的基础上改进的， 在中心系数上使用一个权值2， 相比较Prewitt算子，Sobel模板能够较好的抑制(平滑)噪声。

计算公式：

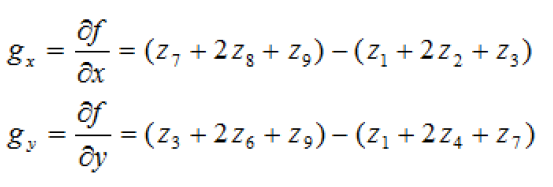
sobel算子：

数学推导：

• sobel算子也有两个，一个是检测水平边缘的模板基于sobel算子的边缘检测，另一个是检测垂直边缘的模板基于sobel算子的边缘检测。
• 与Prewitt算子相比，sobel算子对于像素位置的影响做了加权，因此效果更好。
• sobel算子的另外一种形式是各向同性Sobel算子， 也有两个模板组成，一个是检测水平边缘的基于sobel算子的边缘检测，另一个是检测垂直边缘的基于sobel算子的边缘检测。
• 各向同性Sobel算子和普通sobel算子相比，位置加权系数更为准确，在检测不同方向的边缘是梯度的幅度是一致的。

【Laplace算子：二阶微分算子】

Laplace 算子是一种各向同性算子，在只关心边缘的位置而不考虑其周围的像素灰度差值时比较合适。Laplace算子对孤立像素的响应要比对边缘或线的响应要更强烈， 因此只适合用于无噪声图像。存在噪声情况下， 使用Laplace算子检测边缘之前需要先进行低通滤波。

一阶导数：

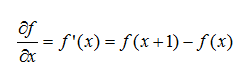
二阶导数：

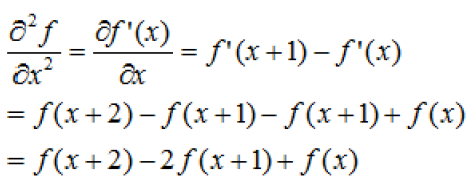
我们需要注意的是关于点x的二阶导数，故将上式中的变量减去1后，得到：

在图像处理中通过拉普拉斯模板求二阶导数， 其定义如下：

写成差分形式为

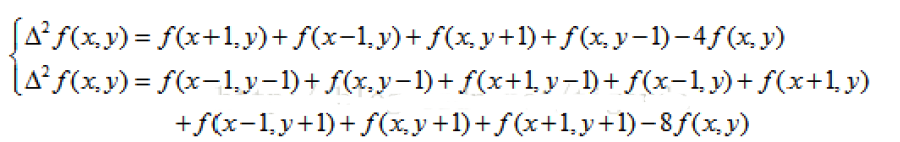
laplace卷积核：

在用lapacian 算子图像进行卷积运算时，当响应的绝对值超过指定阈值时，那么该点就是被检测出来的孤立点，具体输出如下：

【LoG算子：二阶微分算子】

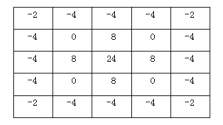
Log 边缘检测则是先进行高斯滤波再进行拉普拉斯算子检测, 然后找过零点来确定边缘位置，很多时候我们只是知道Log 5*5 模板如上图所示。

二维高斯公式：

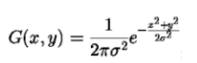
按拉普拉斯算子公式求X，Y方向的二阶偏导后：

这里x，y 不能看成模板位置，应看成是模板其他位置到中心位置的距离。那么写成：

这里x0，y0 就是模板中心位置，x，y 是模板其他位置，对于5*5 模板， 则$x_0,=2 , y_0=2$，那对于模板中（0,0）位置的权值，即把x= 0，y= 0，x0= 2，y0 = 2 带入上式， 令σ= 1，得到约等于0.0175，这样得到

通过取整变符号，且模板总和为0，得到下图所示的模板。

通常高斯分布中，在（-3σ，3σ）的范围内就覆盖了绝大部分区域，所以模板大小一般取dim = 1 + 6σ（在SIFT 特征中，其中的高斯模糊也是这样取），dim 如果为小数，则取不小于dim 的最小整数，当然实际使用时没有这么严格，如上面我们取σ=1 时，模板大小取5*5。那同一个尺寸的模板中的权值调整就是σ的变化得到的，变化到一定程度，模板尺寸大小改变。

Canny算子：非微分算子

【基本原理】

• 图象边缘检测必须满足两个条件:
  • 能有效的抑制噪声。
  • 必须尽量精确确定边缘的位置。
• 根据对信噪比与定位乘积进行测度，，得到最优化逼近算子。这就是Canny边缘检测算子。
• 类似与LoG边缘检测方法，也属于先平滑后求导数的方法。

【算法步骤】

1. 使用高斯滤波器，以平滑图像，滤除噪声。
2. 计算图像中每个像素点的梯度强度和方向。
3. 应用非极大值（Non-Maximum Suppression）抑制， 以消除边缘检测带着的杂散响应。
4. 应用双阈值（Double-Threshold）检测来确定真实的和潜在的边缘。
5. 通过抑制孤立的弱边缘最终完成边缘检测。

第一步：同时平滑与微分

使用高斯函数的一阶导数同时完成平滑和微分。

第二步：计算梯度和方向

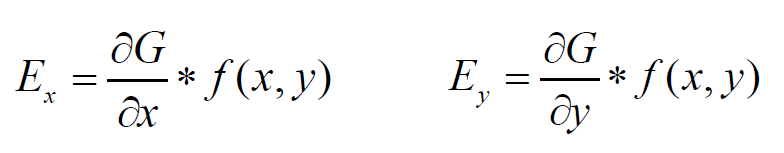
• 梯度幅值和方向

• 方向离散化：离散化为上下左右和斜45°共4个方向

第三步：梯度幅值非极大值抑制

细化梯度幅值图像中的屋脊带，只保留幅值局部变化最大的点

使用一个3*3邻域作用于幅值阵列的所有点。在每一点上, 邻域的中心像素与沿梯度方向的两个梯度幅值的插值结果进行较，仅保留极大值点

第四步：边缘连接

对上一步得到的图像使用低、高阈值t1, t2 阈值化，得到三幅图像

• T1对应假边缘，去除
• T3对应真边缘，全部保留
• T2连接：临接像素中是否有属于T3的像素

第五步：抑制孤立低阈值点

边缘检测总结

1. 边缘检测即图像差分
2. 常见边缘检测算子包括Robert算子，Sobel算子，LoG算子等，其中Sobel算子最为常用
3. Canny算子的基本优点在于检测准确、对噪声稳健，在实际中广泛应用.

代码演示

import cv2
import numpy as np

# 加载图片
image = cv2.imread('lena.jpg')
img = cv2.pyrDown(image)
cv2.imshow("source image", img)


def RobertImage(img, name):
    """
    robert算子的实现
    :param img:
    :param name:
    :return:
    """
    r_sunnzi = np.array([[-1, 1], [1, -1]], np.float32)
    robertImage = cv2.filter2D(img, -1, r_sunnzi)
    cv2.imshow("Robert-%s" % name, robertImage)


def sobelImage(img, name):
    """
    Sobel算子
    Sobel(src, ddepth, dx, dy, dst=None, ksize=None, scale=None, delta=None, borderType=None)
    前四个是必须的参数：
    第一个参数是需要处理的图像；
    第二个参数是图像的深度，-1表示采用的是与原图像相同的深度。目标图像的深度必须大于等于原图像的深度；
    dx和dy表示的是求导的阶数，0表示这个方向上没有求导，一般为0、1、2。
    其后是可选的参数：
    dst不用解释了；
    ksize是Sobel算子的大小，必须为1、3、5、7。
    scale是缩放导数的比例常数，默认情况下没有伸缩系数；
    delta是一个可选的增量，将会加到最终的dst中，同样，默认情况下没有额外的值加到dst中；
    borderType是判断图像边界的模式。这个参数默认值为cv2.BORDER_DEFAULT。
    :param img: 图片数据
    :param name: 命名标志
    :return:
    """
    # 先检测xy方向上的边缘
    Sobel_Ex = cv2.Sobel(src=img, ddepth=cv2.CV_16S, dx=1, dy=0, ksize=3)
    Sobel_Ey = cv2.Sobel(src=img, ddepth=cv2.CV_16S, dx=0, dy=1, ksize=3)
    # 即Sobel函数求完导数后会有负值，还有会大于255的值。而原图像是uint8，即8位无符号数，
    # 所以Sobel建立的图像位数不够，会有截断。因此要使用16位有符号的数据类型，即cv2.CV_16S。
    # cv2.imshow("Sobel_Ex-%s" % name, Sobel_Ex)
    # 图像的每一个像素的横向及纵向梯度近似值结合
    # 用convertScaleAbs()函数将其转回原来的uint8形式。否则将无法显示图像，而只是一副灰色的窗口。
    absX = cv2.convertScaleAbs(Sobel_Ex)
    absY = cv2.convertScaleAbs(Sobel_Ey)
    # cv2.imshow("absX-%s" % name, absX)
    # cv2.imshow("absY-%s" % name, absY)

    SobelImage = cv2.addWeighted(absX, 0.5, absY, 0.5, 0)
    cv2.imshow("sobel-%s" % name, SobelImage)
    # ddepth=-1表示图像深度和原图深度一致
    # Ex = cv2.Sobel(img, -1, 1, 0, ksize=3)
    # Ey = cv2.Sobel(img, -1, 0, 1, ksize=3)
    # # cv2.imshow("Ex-%s" % name, Ex)
    # SobelImg = cv2.addWeighted(Ex, 0.5, Ey, 0.5, 0)
    # cv2.imshow("soImg-%s" % name, SobelImg)


def LaplaceImage(img, name):
    """
    Laplace算子
    Laplacian(src, ddepth, dst=None, ksize=None, scale=None, delta=None, borderType=None)
    前两个是必须的参数：
    第一个参数是需要处理的图像；
    第二个参数是图像的深度，-1表示采用的是与原图像相同的深度。目标图像的深度必须大于等于原图像的深度；
    其后是可选的参数：
    dst不用解释了；
    ksize是算子的大小，必须为1、3、5、7。默认为1。
    scale是缩放导数的比例常数，默认情况下没有伸缩系数；
    delta是一个可选的增量，将会加到最终的dst中，同样，默认情况下没有额外的值加到dst中；
    borderType是判断图像边界的模式。这个参数默认值为cv2.BORDER_DEFAULT。
    :param img: 图片数据
    :param name: 命名标志
    :return:
    """
    # ddepth=-1表示图像深度和原图深度一致
    # laplaceImage = cv2.Laplacian(img, ddepth=-1, ksize=3)
    # cv2.imshow("laplace-%s" % name, laplaceImage)
    # ddepth=cv2.CV_16S表示图像深度
    laplaceImg = cv2.Laplacian(img, ddepth=cv2.CV_16S, ksize=3)
    lapimg = cv2.convertScaleAbs(laplaceImg)
    cv2.imshow("laplace-%s" % name, lapimg)


def LoG(img, name):
    """
    LoG算子的实现
    :param img:
    :param name:
    :return:
    """
    gaussImage = cv2.GaussianBlur(img, (5, 5), 0.01)
    laplaceImg = cv2.Laplacian(gaussImage, ddepth=cv2.CV_16S, ksize=3)
    logImg = cv2.convertScaleAbs(laplaceImg)
    cv2.imshow("LoG-%s" % name, logImg)


def CannyImage(img, name):
    """
    必要参数：
    第一个参数是需要处理的原图像，该图像必须为单通道的灰度图；
    第二个参数是阈值1；
    第三个参数是阈值2。
    其中较大的阈值2用于检测图像中明显的边缘，但一般情况下检测的效果不会那么完美，
    边缘检测出来是断断续续的。所以这时候用较小的第一个阈值用于将这些间断的边缘连接起来。
    :param img: 图片数据
    :param name: 命名标志
    :return:
    """
    # 先进行高斯平滑
    gaussImage = cv2.GaussianBlur(img, (3, 3), 0)
    # 边缘检测，最大阈值为150，最小阈值为50
    # Canny 推荐的 高:低 阈值比在 2:1 到3:1之间。
    cannyImage = cv2.Canny(gaussImage, 50, 150)
    cv2.imshow("canny-%s" % name, cannyImage)


# 彩色图像进行Robert边缘检测
RobertImage(img, 'rgb')
# 灰度图像进行robert边缘检测
grayImage = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
RobertImage(grayImage, 'gray')

# 彩色图像进行sobel边缘检测
sobelImage(img, 'rgb')
# 灰度图像进行sobel边缘检测
grayImage = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
sobelImage(grayImage, 'gray')

# 彩色图像进行laplace边缘检测
LaplaceImage(img, 'rgb')
# 灰度图像进行laplace边缘检测
grayImage = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
LaplaceImage(grayImage, 'gray')

# 彩色图像进行LoG边缘检测
LoG(img, 'rgb')
# 灰度图像进行LoG边缘检测
grayImage = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
LoG(grayImage, 'gray')

# 彩色图像进行canny边缘检测
CannyImage(img, 'rgb')
# 灰度图像进行canny边缘检测
grayImage = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
CannyImage(grayImage, 'gray')

cv2.waitKey(0)

• sobel 产生的边缘有强弱，抗噪性好
• laplace 对边缘敏感，可能有些是噪声的边缘，也被算进来了
• canny 产生的边缘很细，可能就一个像素那么细，没有强弱之分。