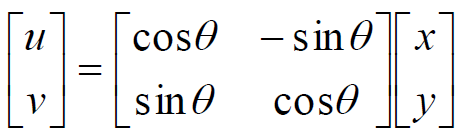坐标变换与摄像机模型

图像变换模型

【平移变换】

只改变图形位置，不改变图形的大小和形状.

代码及演示

import cv2
import numpy as np

# 加载图片
source_image = cv2.imread('lena.jpg', 0)
cv2.imshow('source', source_image)
# 平移图片
rows, cols = source_image.shape
# 创建交换矩阵，按（100,50）平移
M = np.float32([[1, 0, 100], [0, 1, 50]])
# 使用仿射变换的api进行平移变换
translation_image = cv2.warpAffine(source_image, M, (cols, rows))
cv2.imshow('translation', translation_image)

cv2.waitKey(0)

【旋转变换】

将输入图像绕笛卡尔坐标系的原点逆时针旋转$\theta$角度， 则变换后图像坐标为

代码及演示

import cv2
import numpy as np

# 加载图片
source_image = cv2.imread('lena.jpg', 0)
cv2.imshow('source', source_image)
# 获取形状
rows, cols = source_image.shape
# 旋转图片
# 创建交换矩阵， 旋转90度
M = cv2.getRotationMatrix2D(((cols-1)/2., (rows-1)/2.), 90, 1)
# 使用仿射变换的api进行旋转变换
rotation_image = cv2.warpAffine(source_image, M, (cols, rows))
cv2.imshow('rotation', rotation_image)
cv2.waitKey(0)

【比例变换】

若图像坐标$(x, y)$ 缩放到$(S_x, S_y)$倍，则变换函数为：

其中$S_y$, 分别为 x和y 坐标的缩放因子，其大于1表示放大，小于1表示缩小。

代码及演示

import cv2
import numpy as np

# 加载图片
source_image = cv2.imread('lena.jpg', 0)
cv2.imshow('source', source_image)
# 获取形状
rows, cols = source_image.shape
# 比例变换
# 缩小一半
proportion_image = cv2.resize(source_image, (cols//2, rows//2), cv2.INTER_CUBIC)
cv2.imshow('proportion', proportion_image)

cv2.waitKey(0)

【仿射变换】

简单的来说就是一个线性变换加上平移

仿射变换的一般表达式为:

平移、比例缩放和旋转变换都是一种称为仿射变换的特殊情况。

仿射变换的性质

• 仿射变换有6个自由度（对应变换中的6个系数），因此，仿射变换后互相平行直线仍然为平行直线，三角形映射后仍是三角形。但却不能保证将四边形以上的多边形映射为等边数的多边形。
• 仿射变换，可以保持原来的线共点，点共线的关系不变，保持原来相互平行的的先仍然相互平行，保持原来在一直线上几段线段之间的比例 关系不变。但是，仿射变换不能保持原来的线段长度不变，也不能保持原来的夹角角度不变。
• 仿射变换的乘积和逆变换仍是仿射变换。
• 仿射变换能够实现平移、旋转、缩放等几何变换。

代码及演示

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 加载图片
source_image = cv2.imread('lena.jpg', 0)

cv2.imshow('source', source_image)
# 获取形状
rows, cols = source_image.shape
# 仿射变换
# 定义交换矩阵
pts1 = np.float32([[50, 50], [200, 50], [50, 200]])
pts2 = np.float32([[10, 100], [200, 50], [100, 250]])
M = cv2.getAffineTransform(pts1, pts2)
# 开始变换
affine_image = cv2.warpAffine(source_image, M, (cols, rows))
plt.subplot(121), plt.imshow(source_image), plt.title('Input')
plt.subplot(122), plt.imshow(affine_image), plt.title('Output')
plt.show()
cv2.imshow('affine', affine_image)

cv2.waitKey(0)

【透视变换】

• 把物体的三维图像表示转变为二维表示的过程，称为透视变换，也称为投影映射，其表达式为:

• 透视变换也是一种平面映射 ，并且可以保证任意方向上的直线经过透视变换后仍然保持是直线。
• 透视变换具有9个自由度（其变换系数为9个），故可以实现平面四边形到四边形的映射。

透视变化示意

对于透视投影，一束平行于投影面的平行线的投影可保持平行，而不平行于投影面的平行线的投影会聚集到一个点，该点称灭点.

代码及演示

import cv2
import numpy as np
import matplotlib.pyplot as plt

# 加载图片
source_image = cv2.imread('lena.jpg', 0)

cv2.imshow('source', source_image)
# 获取形状
rows, cols = source_image.shape
# 透视变换
# 定义交换矩阵
pts1 = np.float32([[56, 65], [368, 52], [28, 387], [389, 390]])
pts2 = np.float32([[0, 0], [300, 0], [0, 300], [300, 300]])
M = cv2.getPerspectiveTransform(pts1, pts2)
# 开始变换
perspective_image = cv2.warpPerspective(source_image, M, (300, 300))

plt.subplot(121), plt.imshow(source_image), plt.title('Input')
plt.subplot(122), plt.imshow(perspective_image), plt.title('Output')
plt.show()
cv2.imshow('perspective', proportion_image)
cv2.waitKey(0)

坐标系和坐标变换

• 不同坐标系及坐标变换关系

  当物体旋转时，其上的点在固定坐标系坐标值变化。

• 任意两个三维坐标系之间的变换关系

  

  注意：R满足旋转矩阵正交性约束

• 坐标系变换及旋转矩阵生成示意图

  

【像素坐标系】

像素坐标系uov是一个二维直角坐标系，反映了相机CCD/CMOS芯片中像素的排列情况。原点o位于图像的左上角，u轴、v轴分别于像面的两边平行。像素坐标系中坐标轴的单位是像素（整数）。

【图像坐标系】

图像坐标系(x,y)：像素坐标系不利于坐标变换，因此需要建立图像坐标系XOY，其坐标轴的单位通常为毫米（mm），原点是相机光轴与相面的交点（称为主点），即图像的中心点，X轴、Y轴分别与u轴、v轴平行。故两个坐标系实际是平移关系，即可以通过平移就可得到。

【摄像机坐标系】

相机坐标系（camera coordinate）($O_cX_cY_cZ_c (camera frame)$)，也是一个三维直角坐标系，原点位于镜头光心处，x、y轴分别与相面的两边平行，z轴为镜头光轴，与像平面垂直。

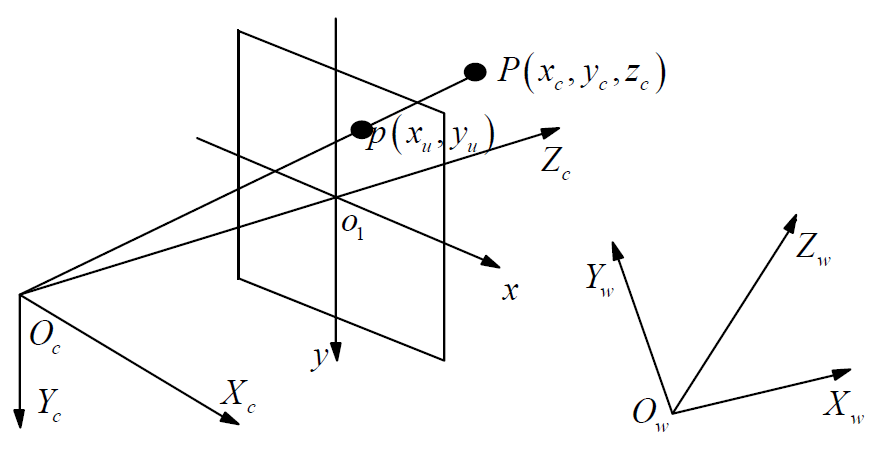
【世界坐标系】

世界坐标系（world coordinate）($O_wX_wY_wZ_w$)，也称为测量坐标系，是一个三维直角坐标系，以其为基准可以描述相机和待测物体的空间位置。世界坐标系的位置可以根据实际情况自由确定。

【手端坐标系或平台坐标系】

$O_eX_eY_eZ_e$

【目标坐标系】

$O_tX_tY_tZ_t$

【坐标系转换】

• 世界坐标系转换为相机坐标系

  

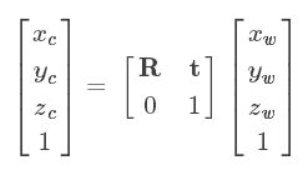
其中R为3*3的旋转矩阵，t为3*1的平移矢量，即相机外参数

• 相机坐标系转换为图像坐标系

  

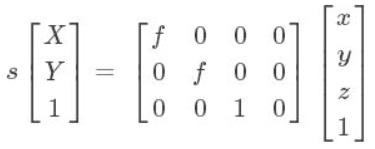
  s为比例因子（s不为0），f为有效焦距（光心到图像平面的距离），(x,y,z,1)是空间点P在相机坐标系oxyz中的齐次坐标，(X,Y,1)是像点p在图像坐标系OXY中的齐次坐标。

• 图像坐标系转换为像素坐标系

  

  其中，dX、dY分别为像素在X、Y轴方向上的物理尺寸，$u_0,v_0$为主点（图像原点）坐标

• 世界坐标系转换为像素坐标系

  

  其中，$m_1、m_2$即为相机的内参和外参数。

  注意：R,t参数矩阵为不可逆矩阵。

线性及非线性摄像机模型

【线性摄像机模型】

• 考虑简化的针孔模型

  ​ 针孔模型是各种相机模型中最简单的一种，它是相机的一个近似线性模型。在相机坐标系下，任一点$P(X_c,Y_c,Z_c)$在像平面的投影位置,也就是说，任一点$P(X_c,Y_c,Z_c)$的投影点p(x,y)都是OP（即光心（投影中心）与点$P(X_c,Y_c,Z_c)$的连线）与像平面的交点如下图。

  

  

• 加入相机坐标系与世界坐标系变换关系，得到

  

  

说明：上述公式中完成了从世界坐标系到图像坐标系的转变，中间经过了相机坐标系的过度，$X_w$中的w表示world世界，单位为毫米，而u,v是的 单位为像素，即完成了从毫米——像素的转换。

所以，为了得到空间物体的三维世界坐标，就必须有两个或更多的相机构成立体视觉系统模型才能实现。

成像畸变示意

【非线性摄像机模型】

在实际的成像过程中，考虑镜头的失真，一般都存在非线性畸变，所以线性模型不能准确描述成像几何关系。非线性畸可用下列公式描述：

• 径向畸变，离心畸变，薄棱镜畸变

  通常只考虑径向畸变：

  

• 若考虑非线性畸变，则对相机标定时需要使用非线性优化算法。而有研究表明引入过多的非线性参入（如离心畸变和薄棱畸变）不仅不能提高精度，还会引起解的不稳定。一般情况下径向畸变就足以描述非线性畸变，所有本课题只是考虑径向畸变。则将式(2.9)中的径向畸变代入式(2.8)可得：

  

总结

• 图像变换包括平秱、旋转、仿射、透视变换等
• 常用的坐标系包括像素坐标系、相机坐标系、世界坐标系等，任一点在世界坐标系和相机坐标系中的坐标通过投影矩阵M相关联，M包含了内参数和外参数矩阵
• 一般相机成像存在非线性畸变，重点需要考虑径向畸变