相机标定

【基本问题】

• 相机内外参数标定

  

  • 计算$m_{ij}$的解
  • 分解内、外参数
  • 考虑非线性项

【Zhang方法】

• Zhang方法：由张正友提出，OpenCV等广泛使用

  • 特点：使用平面靶标摆多个pose(可未知)
  • 标定步骤
    • 对一个pose,计算单应矩阵(类似M矩阵)
    • 有三个以上Pose，根据各单应矩阵计算线性相机参数；
    • 使用非线性优化方法计算非线性参数

• 第一步：求解单应矩阵——基本方程

  • 特点：使用平面靶标摆多个pose(可未知)

    

  • 平面靶标有四个点或更多时，可求解H(差一比例因子)

• 第二步：求解单应矩阵——建立内参数方程

  

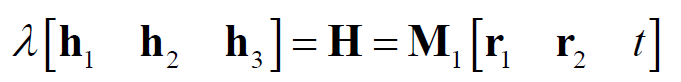
  • 根据R约束

    

  • 对应每一个pose,可得到上述两个方程

• 第三步：求解内参数——建立方程

  • 令 $B=(b_{ij})=M_1^{-T}M_1^{-1}$

  • 根据B对称，定义参数向量

    

• 第四步：求解参数——建立内参数方程

  

• 第五步：求解参数——内参数求解

  • 当n>=3 时,可求解b

    

  • 解为：

    

  • 前式代入，可知：

    

  • 进一步可确定$M_1$各参数

• 第六步：求解参数——外参数求解

  

  • 系数

    

• 最后一步：非线性畸变参数求解

  • 以已有解为初值，求解下式：

    

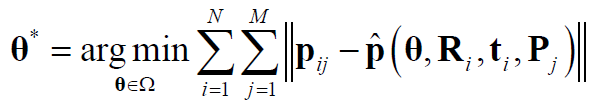
    可使用Levenberg-Marquardt算法求解(原方法中只含径向畸变)

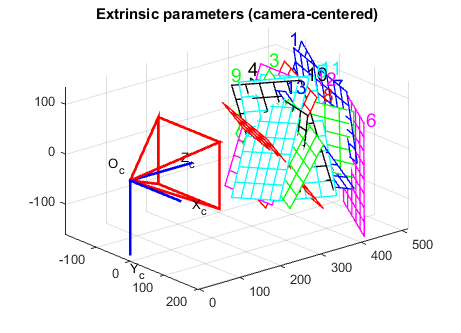
外参数标定结果示意

重投影示意

【总结】

• Zhang方法从多个角度拍摄平面标定物，进一步通过特征点计算内、外参数及非线性畸变
• 与已有方法相比，Zhang方法简单，不需要已知目标特征点三维坐标，因而得到广泛应用
• 注意：参与标定的数据一般为30张左右。

代码演示

#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time    : 2019/2/26 20:15
# @Author  : Seven
# @File    : CameraCalibration.py
# @Software: PyCharm
# function : 摄像机标定
import cv2
import numpy as np
import glob

# 设置寻找亚像素角点的参数，采用的停止准则是最大循环次数30和最大误差容限0.001
criteria = (cv2.TERM_CRITERIA_EPS + cv2.TERM_CRITERIA_MAX_ITER, 30, 0.001)
# 准备目标点，例如 (0,0,0), (1,0,0), (2,0,0) ....,(6,5,0)
objp = np.zeros((6 * 7, 3), np.float32)
# 将世界坐标系建在标定板上，所有点的Z坐标全部为0，所以只需要赋值x和y
objp[:, :2] = np.mgrid[0:7, 0:6].T.reshape(-1, 2)

# 用于存储所有图像中的对象点和图像点的数组。
objpoints = []  # 存储在现实世界空间的3d点
imgpoints = []  # 储存图像平面中的2d点。
images = glob.glob('image/*.jpg')
for fname in images:
    img = cv2.imread(fname)
    gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
    # 获取XY坐标
    size = gray.shape[::-1]
    # 找到棋盘角点
    ret, corners = cv2.findChessboardCorners(gray, (7, 6), None)
    # 如果找到，添加3D点，2D点
    if ret:
        objpoints.append(objp)
        # 增加角点的准确度
        corners2 = cv2.cornerSubPix(gray, corners, (11, 11), (-1, -1), criteria)
        imgpoints.append(corners2)
        # 画出并显示角点
        img = cv2.drawChessboardCorners(img, (7, 6), corners2, ret)
        cv2.imshow('img', img)
        cv2.waitKey(500)
# 相机标定
ret, mtx, dist, rvecs, tvecs = cv2.calibrateCamera(objpoints, imgpoints, size, None, None)
# 保存相机参数
np.savez('C.npz', mtx=mtx, dist=dist, rvecs=rvecs, tvecs=tvecs)
print("ret:", ret)
print("内参数矩阵:\n", mtx)
print("畸变系数:\n", dist)
print("旋转向量:", rvecs)  # 外参数
print("平移向量:", tvecs)  # 外参数

运行结果：