本文最后更新于：14 天前

贝叶斯网络的概念

把某个研究系统中涉及的随机变量，根据是否条件独立绘制在一个有向图中，就形成了贝叶斯网络。

贝叶斯网络(Bayesian network)，又称信念网络(Belief Network)，或有向无环图模型。是一种概率图模型，根据概率图的拓扑结构，考察一组随机变量${ X_1,X_2…X_n}$及其n组条件概率分布的性质。也就是说它用网络结构代表领域的基本因果知识。  

贝叶斯网络的形式化定义

  • $BN(G,Θ)$: 贝叶斯网络(Bayesian Network)

    • $G$:有向无环图 (Directed Acyclic Graphical model, DAG)

    • $G$的结点:随机变量$X_1,X_2…X_n$

    • $G$的边:结点间的有向依赖

    • $Θ$:所有条件概率分布的参数集合

    • 结点X的条件概率: $P(X |parent(X))$

      $P(S,C,B,X,D)=P(S)P(C \mid S)P(B \mid S)P(X \mid C,S)P(D \mid C,B)$

每个结点所需参数的个数:

若结点的$parent$数目是$M$,结点和$parent$的可取值数目都是$K:K^M∗(K−1)$

一个简单的贝叶斯网络

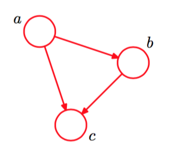
image

$P(a,b,c)=P(c \mid a,b)P(a,b)=P(c \mid a,b)P(b \mid a)P(a)$

全连接贝叶斯网络

每一对结点之间都有边连接

$p(x_1,…x_n)=p(x_K \mid x_1,…,x_{K-1})…p(x_2 \mid x_1)p(x_1)$

$P(X_1=x_1,…,X_n=x_n)=\prod_{i=1}^nP(X_i=x_i \mid X_{i+1},…,X_n=x_n)$

一个”正常“的贝叶斯网络

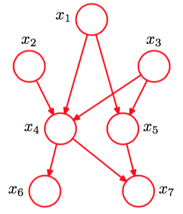
image

从图中我们可以看出：

  • 有些边是缺失的

  • 直观上来看：$x_1,x_2$是相互独立的

  • 直观上来看：$x_6,x_7$在$x_4$给定的条件下独立

  • $x_1,x_2,…x_7$的联合分布：

    $P(x_1)P(x_2)P(x_3)P(x_4\mid x_1, x_2, x_3)P(x_5\mid x_1, x_3)P(x_6\mid x_4)P(x_7\mid x_4, x_5)$

贝叶斯网络的条件独立判定

我们来看一下贝叶斯网络的条件是如何判定的：

  1. 条件独立：tail-to-tail

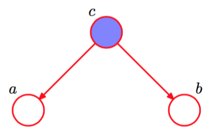
    image

    根据图模型，得：$P(a,b,c)=P(c)P(a \mid c)P(b \mid c)$

    从而：$P(a,b,c)/P(c)=P(a \mid c)P(b \mid c)$

    因为$P(a,b \mid c)=P(a,b,c)/P(c)$

    得：$P(a,b\mid c)=P(a\mid c)P(b\mid c)$

    解释：在c给定的条件下，因为a,b被阻断（blocked），因此是独立的：$P(a,b\mid c)=P(a\mid c)P(b\mid c)$

  1. 条件独立：head-to-tail

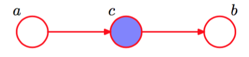
    image

    根据图模型，得：$P(a,b,c)=P(a)P(c \mid a)P(b \mid c)$

    $P(a,b \mid c) \\ =P(a,b,c)/P(c) \\ =P(a)P(c \mid a)P(b \mid c) / P(c) \\ =P(a,c)P(b \mid c) / P(c) \\ = P(a\mid c)P(b\mid c)$

    解释：在c给定的条件下，因为a,b被阻断（blocked），因此是独立的：$P(a,b\mid c)=P(a\mid c)P(b\mid c)$

  1. 条件独立：head-to-head

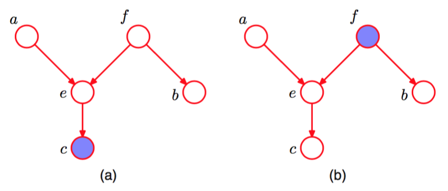
    image

    根据图模型，得：$P(a,b,c)=P(a)P(b)P(c \mid a,b) $

    由：$\sum_c P(a,b,c)= \sum_n P(a)P(b)P(c \mid a,b)$

    得：$P(a,b)=P(a)P(b)$

    解释：在c给定的条件下，因为a,b被阻断（blocked），因此是独立的：$P(a,b)=P(a)P(b)$

有向分离

对于任意的结点集,有向分离(D-separation): 对于任意的结点集A,B,C,考察所有通过A中任意结点到B中任意结点的路径,若要求A,B条件独立,则需要所有的路径都被阻断(blocked),即满足下列两个前提之一:

  1. A和B的head-to-tail型和tail-to-tail型路径都通过C;
  2. A和B的head-to-head型路径不通过C以及C的子孙结点;

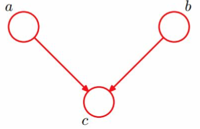
image

图(a), 在tail-to-tail中, f没有阻断; 在head-to-head中, e阻断, 然而它的子结点c没有阻断, 即e所在的结点集没有阻断; 因此, 结点a, b关于c不独立.

图(b), 在tail-to-tail中, f阻断; 因此, 结点a,b关于f 独立. 在head-to-head中, e和它的子孙结点c都阻断; 因此, 结点a,b关于e独立.

特殊的贝叶斯网络

  1. 马尔科夫模型

    image

    结点形成一条链式网络，这种按顺次演变的随机过程模型就称作马尔科夫模型

    $A_{i+1}$只与$A_i$有关，与$A_1,…,A_{i-1}$无关。

  2. 隐马尔科夫模型

    Hidden Markov Model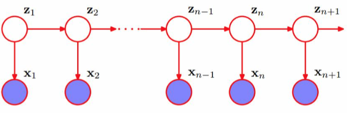

    image

    • 隐马尔科夫模型（HMM）可用标注问题，在语音识别、NLP、生物信息、模式识别等领域别实践证明的有效算法。
    • HMM是关于时序的概率模型，描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列，再由各个状态生成一个观测而产生观测随机序列的过程。
    • HMM随机生成的状态的序列，成为状态序列，每个状态生成一个观测，由此产生的观测随机序列，称为观测序列
      • 序列的每一个位置可看做是一个时刻。
      • 空间序列也可以使用该模型.

  1. 马尔科夫毯

    一个结点的*Markov Blanket *是一个集合，在这个集合中的结点都给定条件下，该结点条件独立于其他结点。

    *Markov Blanket *: 一个结点的Markov Blanket是它的parents,children以及spouses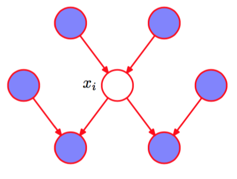

    image

深色的结点集合，就是“马尔科夫毯”（**`Markov Blanket` **）