本文最后更新于:14 天前
感知器–神经网络的起源
神经网络是由人工神经元组成的。我们先来看看人的神经元是什么构造:
感知器是激活函数为阶跃函数的神经元。感知器的模型如下:
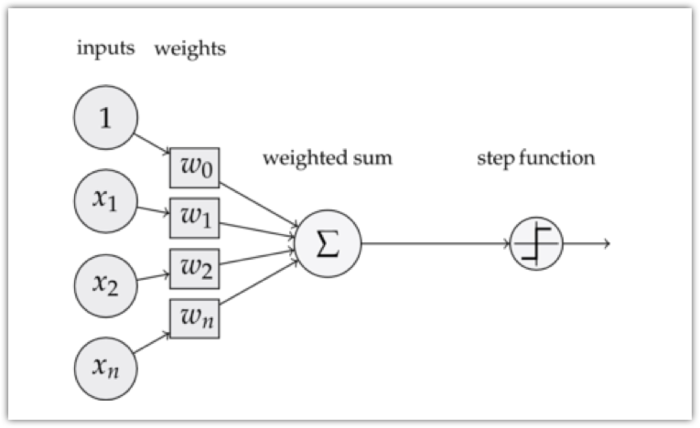
是不是感觉很一样啊 ,神经元也叫做感知器。感知器算法在上个世纪50-70年代很流行,也成功解决了很多问题。并且,感知器算法也是非常简单的。
感知器的定义

我们再来分析下上图这个感知器,可以看到,一个感知器有如下几个组成部分:
- 输入(inputs):一个感知器可以接收多个输入$(x_1,x_2,…,x_n \vert x_i \in R)$
- 权值(weights):每一个输入上都有一个
权值$w_i \in R$,此外还有一个偏置项$b \in R$,也就是上图的$w_0$。 - 加权和(weighted sum):就是
输入权值 xx权值 w+偏置项 b的总和。 - 激活函数(step function):感知器的激活函数:$f(x)=\begin{cases} 0& x>0 \ 1& x \le 0 \end{cases}$
- 输出(output):感知器的输出由
加权值用激活函数做非线性变换。也就是这个公式:$y=f(w\cdot x +b )$
举个栗子:
我们使用unit激活函数结合上图就有:
$y=f(w\cdot x +b )=f(w_1x_1+w_2x_2+w_3x_3+bias)$
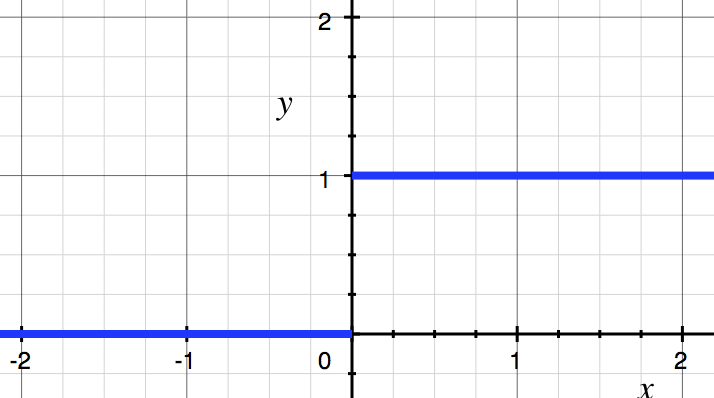
其中$f(x)$就是激活函数 $f(x)= \begin{cases} 1& x>0 \ 0& x \le 0 \end{cases}$ ,图像如下图所示。
感知器的前馈计算
再举个栗子:我们来计算下这个感知器:

其中激活函数f:$f(x)= \begin{cases} 1& x>0 \ 0& x \le 0 \end{cases}$
加权和:logits = 1.0 * (-0.2) + 0.5 * (-0.4) + (-1.4) * 1.3 + 2.0 * 3.0 = 1.98输出值:output = f(logits) = f(1.98) = 1
如果数据很多呢,我们就要把数据向量化:
例如:
$x_1=[-1.0, 3.0, 2.0] \\ x_2=[2.0, -1.0, 5.0] \\ x_3=[-2.0, 0.0, 3.0 ] \\ x_4=[4.0, 1.0, 6.0] \\ w=[4.0, -3.0, 5.0 ] \\ b=2.0$
则:$X=\begin{bmatrix} -1.0 & 3.0 & 2.0 \\ 2.0 & -1.0& 5.0 \\ -2.0& 0.0& 3.0 \\ 4.0& 1.0 & 6.0 \end{bmatrix}$
$w^T =\begin{bmatrix} 4.0 \\ -3.0 \\ 5.0 \end{bmatrix}$
所以:$logits = X\cdot w^T + b= \begin{bmatrix} -1.0 & 3.0 & 2.0 \\ 2.0 & -1.0& 5.0 \\ -2.0& 0.0& 3.0 \\ 4.0& 1.0 & 6.0 \end{bmatrix} \cdot \begin{bmatrix} 4.0 \\ -3.0 \\ 5.0 \end{bmatrix} + 2.0 \\ =[-1.0 \ \ \ 38.0 \ \ \ 7.0 \ \ \ 43.0 ]$
最后带入激活函数:
则:$output = f(x)=[0\ \ \ 1 \ \ \ 1 \ \ \ 1 ]$
感知器的运用
使用感知器可以完成一些基础的逻辑操作
例如逻辑与
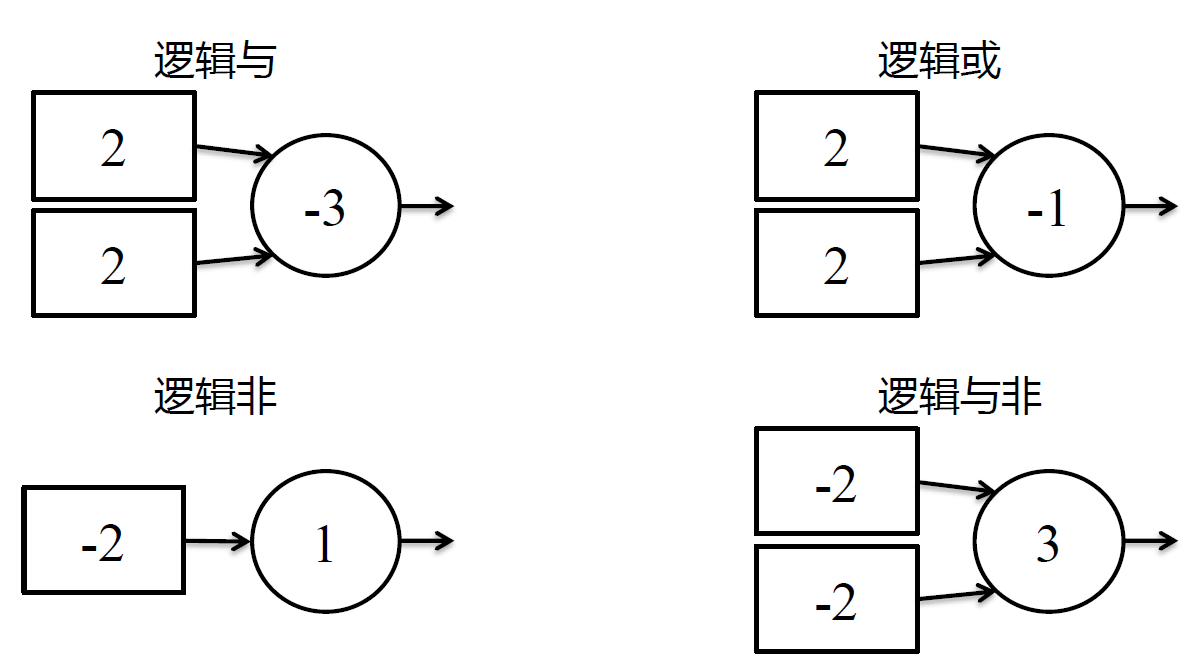
注意:激活函数是unit激活函数,再看看其他逻辑运算

感知器的局限性
- 仅能做0-1输出
- 仅能处理线性分类的问题(无法处理XOR问题)
多层感知机–现代神经网络的原型
对比于感知器,引入了隐层,改变了激活函数,加入反向传播算法,优化算法,也就是后面要讲的神经网络。
隐层的定义

从上图中可以看出:
- 所有同一层的神经元都与上一层的每个输出相连
- 同一层的神经元之间不相互连接
- 各神经元的输出为数值
隐层的结构
举个栗子:
由上图可知:
$h_1 = f(2x_1+2x_2-1) \\ h_2=f(-2x_1+-2x_2+3) \\ o_1 = f(2h_1+2h_2-3)$
其中$f(x)$是激活函数
激活函数
新的激活函数:
unit激活函数:$f(x)=unit(x)= \begin{cases} 0& x>0 \ 1& x \le 0 \end{cases} $
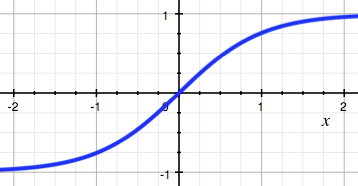
sigmod激活函数:$f(x)=sigmod(x)=\frac{1}{1+e^{-x}}$
tanh激活函数:$f(x)=tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$
 `
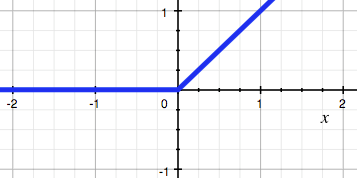
`ReLU激活函数:$f(x)=ReLU(x)=\begin{cases} x& x>0\ 0& x \le 0 \end{cases} $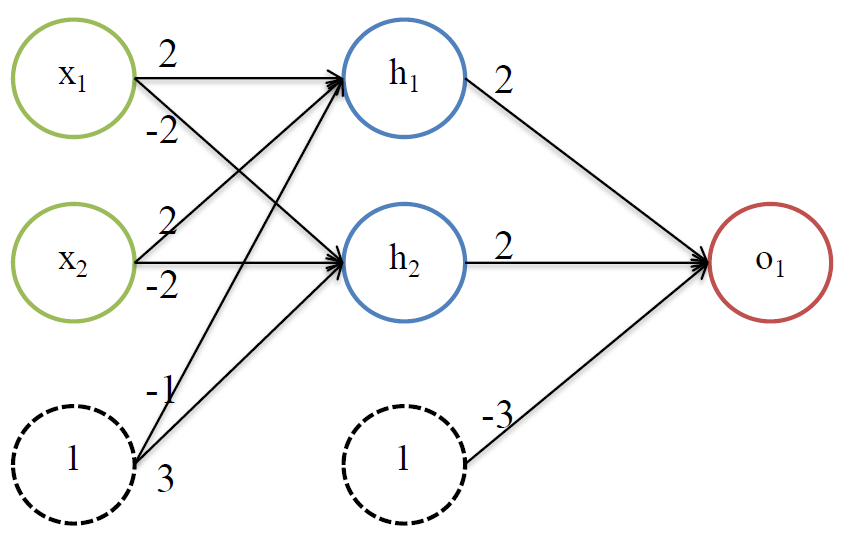
激活函数的作用
引入非线性因素。
在我们面对线性可分的数据集的时候,简单的用线性分类器即可解决分类问题。但是现实生活中的数据往往不是线性可分的,面对这样的数据,一般有两个方法:引入非线性函数、线性变换。
线性变换
就是把当前特征空间通过一定的线性映射转换到另一个空间,让数据能够更好的被分类。
激活函数的特点
unit:线性分界– 几乎已经不用了
sigmoid:非线性分界– 两端软饱和,输出为 (0,1)区间
– 两端有梯度消失问题
– 因为输出恒正,可能有 zig现象
tanh:非线性分界 :非线性分界– 两端软饱和,输出为 (-1, 1) 区间
– 仍然存在梯度消失问题
– 没有 zig,收敛更快 (LeCun 1989)
ReLU:非线性分界
– 左侧硬饱和,右无输出为 [0,+∞)区间– 左侧会出现梯度一直为 0的情况,导致神经元 不再更新(死亡)
– 改善了梯度弥散
– 同样存在 zig
一些新的激活函数
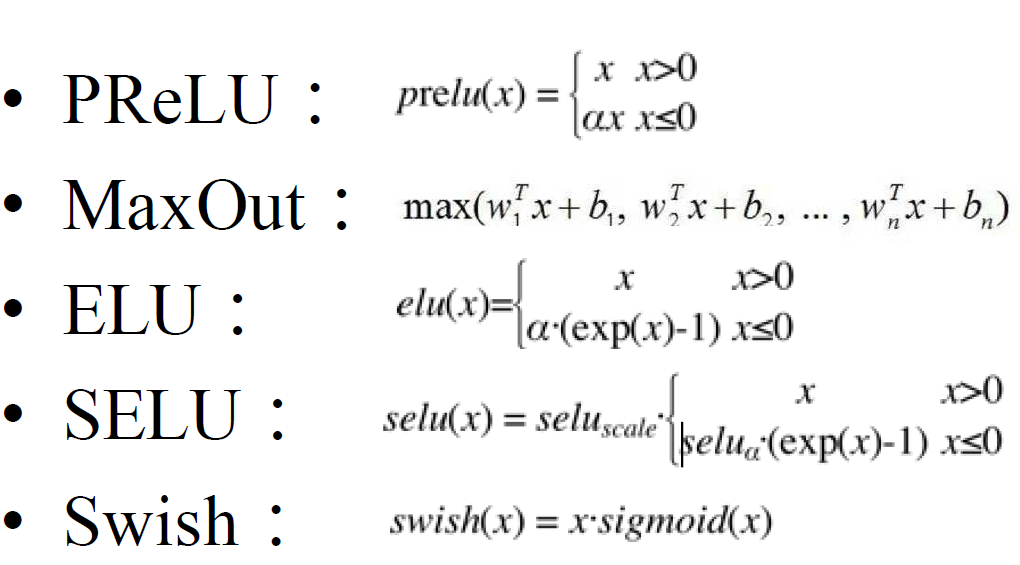
本博客所有文章除特别声明外,均采用 CC BY-SA 3.0协议 。转载请注明出处!