PYTHON实现RNN算法

实现学习二进制的加法。

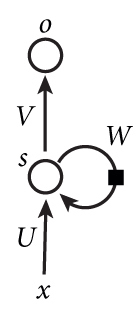
如上图所示，我们来手写RNN算法：

代码：

#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time    : 2018/8/29 13:51
# @Author  : Seven
# @Site    :
# @File    : demo.py
# @Software: PyCharm

# TODO:导入环境
import copy
import numpy as np
np.random.seed(0)


# 使用SIGMOD函数转换成非线性
def sigmoid(inputs):
    output = 1 / (1 + np.exp(-inputs))
    return output


# 将SIGMOD函数的输出转换成其导数
def sigmoid_output_to_derivative(output):
    return output * (1 - output)


# TODO: 生成训练数据集-->把十进制转换为8位二进制
int2binary = {}
binary_dim = 8

largest_number = pow(2, binary_dim)  # 2**8=256

# 把0-256转换成对应的二进制编码并储存起来
binary = np.unpackbits(
    np.array([range(largest_number)], dtype=np.uint8).T, axis=1)

for i in range(largest_number):
    int2binary[i] = binary[i]

# 参数定义
alpha = 0.1
input_dim = 2
hidden_dim = 16
output_dim = 1

# 初始化权重参数--在-1到1之间
U = 2 * np.random.random((input_dim, hidden_dim)) - 1
V = 2 * np.random.random((hidden_dim, output_dim)) - 1
W = 2 * np.random.random((hidden_dim, hidden_dim)) - 1

# 更新权重参数
U_update = np.zeros_like(U)
V_update = np.zeros_like(V)
W_update = np.zeros_like(W)

# TODO:训练
for step in range(10000):

    # 随机生成一个加法a+b=c（因为最大是8位，所以a最大是largest_number的1/2）
    a_int = np.random.randint(largest_number / 2)  # int version
    a = int2binary[a_int]  # binary encoding

    b_int = np.random.randint(largest_number / 2)  # int version
    b = int2binary[b_int]  # binary encoding

    # true answer
    c_int = a_int + b_int
    c = int2binary[c_int]

    # 存储概率最大的二进制--预测值
    d = np.zeros_like(c)

    overallError = 0

    out_deltas = list()
    layer_1_values = list()  # 保存’记忆‘
    layer_1_values.append(np.zeros(hidden_dim))

    # 沿着二进制的位置移动--前向传播
    for position in range(binary_dim):
        # 生成输入和输出的值
        X = np.array([[a[binary_dim - position - 1], b[binary_dim - position - 1]]])
        y = np.array([c[binary_dim - position - 1]]).T

        # hidden layer --> UX+layer1·W
        layer_1 = sigmoid(np.dot(X, U) + np.dot(layer_1_values[-1], W))

        # output layer
        layer_2 = sigmoid(np.dot(layer_1, V))

        # 计算损失值
        layer_2_error = y - layer_2
        out_deltas.append(layer_2_error * sigmoid_output_to_derivative(layer_2))
        overallError += np.abs(layer_2_error[0])

        # 解码成十进制
        d[binary_dim - position - 1] = np.round(layer_2[0][0])

        # 保存记忆，以便下一时刻使用
        layer_1_values.append(copy.deepcopy(layer_1))

    future_layer_1_delta = np.zeros(hidden_dim)

    # 反向传播
    for position in range(binary_dim):
        X = np.array([[a[position], b[position]]])
        layer_1 = layer_1_values[-position - 1]
        prev_layer_1 = layer_1_values[-position - 2]

        # error at output layer
        layer_2_delta = out_deltas[-position - 1]
        # error at hidden layer
        layer_1_delta = (future_layer_1_delta.dot(W.T) + layer_2_delta.dot(
            V.T)) * sigmoid_output_to_derivative(layer_1)

        # 更新权重参数
        V_update += np.atleast_2d(layer_1).T.dot(layer_2_delta)
        W_update += np.atleast_2d(prev_layer_1).T.dot(layer_1_delta)
        U_update += X.T.dot(layer_1_delta)

        future_layer_1_delta = layer_1_delta

    U += U_update * alpha
    V += V_update * alpha
    W += W_update * alpha

    U_update *= 0
    V_update *= 0
    W_update *= 0

    # print out progress
    if step % 1000 == 0:
        print("错误值:" + str(overallError))
        print("预测值:" + str(d))
        print("正确值:" + str(c))
        out = 0
        for index, x in enumerate(reversed(d)):
            out += x * pow(2, index)
        print(str(a_int) + " + " + str(b_int) + " = " + str(out))
        print("------------")

结果：

损失值:[3.45638663]
预测值:[0 0 0 0 0 0 0 1]
正确值:[0 1 0 0 0 1 0 1]
9 + 60 = 1
------------
损失值:[3.63389116]
预测值:[1 1 1 1 1 1 1 1]
正确值:[0 0 1 1 1 1 1 1]
28 + 35 = 255
------------
损失值:[3.91366595]
预测值:[0 1 0 0 1 0 0 0]
正确值:[1 0 1 0 0 0 0 0]
116 + 44 = 72
------------
损失值:[3.72191702]
预测值:[1 1 0 1 1 1 1 1]
正确值:[0 1 0 0 1 1 0 1]
4 + 73 = 223
------------
损失值:[3.5852713]
预测值:[0 0 0 0 1 0 0 0]
正确值:[0 1 0 1 0 0 1 0]
71 + 11 = 8
------------
损失值:[2.53352328]
预测值:[1 0 1 0 0 0 1 0]
正确值:[1 1 0 0 0 0 1 0]
81 + 113 = 162
------------
损失值:[0.57691441]
预测值:[0 1 0 1 0 0 0 1]
正确值:[0 1 0 1 0 0 0 1]
81 + 0 = 81
------------
损失值:[1.42589952]
预测值:[1 0 0 0 0 0 0 1]
正确值:[1 0 0 0 0 0 0 1]
4 + 125 = 129
------------
损失值:[0.47477457]
预测值:[0 0 1 1 1 0 0 0]
正确值:[0 0 1 1 1 0 0 0]
39 + 17 = 56
------------
损失值:[0.21595037]
预测值:[0 0 0 0 1 1 1 0]
正确值:[0 0 0 0 1 1 1 0]
11 + 3 = 14
------------