本文最后更新于:14 天前
递归神经网络
递归神经网络(Recurrent Neural Networks,RNN)是两种人工神经网络的总称:
时间递归神经网络(recurrent neural network):时间递归神经网络的神经元间连接构成有向图
结构递归神经网络(recursive neural network):结构递归神经网络利用相似的神经网络结构递归构造更为复杂的深度网络。
递归神经网络(RNN)(也叫循环神经网络)是一类神经网络,包括一层内的加权连接,与传统前馈神经网络相比,加权连接仅反馈到后续层。因为RNN包含循环,所以RNN就可以在处理输入信息的时候同时储存信息。这种记忆使得RNN非常适合处理必须考虑事先输入的任务(比如时序数据)。所以循环神经网络在自然语言处理领域非常适合。
RNN一般指代时间递归神经网络。单纯递归神经网络因为无法处理随着递归,权重指数级爆炸或消失的问题(Vanishing gradient problem),难以捕捉长期时间关联;而结合不同的LSTM可以很好解决这个问题。时间递归神经网络可以描述动态时间行为,因为和前馈神经网络(feedforward neural network)接受较特定结构的输入不同,RNN将状态在自身网络中循环传递,因此可以接受更广泛的时间序列结构输入。
语言模型
RNN是在自然语言处理领域中最先被用起来的,比如,RNN可以为语言模型来建模。
我们小时候都做过语文的填空题吧
饿死了,我要吃__。如果是我,肯定是填肉。哈哈
但是我不是今天的主角,如果这个问题我们让计算机来回答呢?
我们给计算机展示这段话,让计算机给出答案。而这个答案最有可能的就是饭,而太可能是睡觉或者做作业.
语言模型就是这样的东西:给定一个一句话前面的部分,预测接下来最有可能的一个词是什么。
语言模型是对一种语言的特征进行建模,它有很多很多用处。比如在语音转文本(STT)的应用中,声学模型输出的结果,往往是若干个可能的候选词,这时候就需要语言模型来从这些候选词中选择一个最可能的。当然,它同样也可以用在图像到文本的识别中(OCR)。
使用RNN之前,语言模型主要是采用N-Gram。N可以是一个自然数,比如2或者3。它的含义是,假设一个词出现的概率只与前面N个词相关。我们以2-Gram为例。首先,对前面的一句话进行切词:
饿死了,我要____。如果用2-Gram进行建模,那么电脑在预测的时候,只会看到前面的『要』,然后,电脑会在语料库中,搜索『要』后面最可能的一个词。不管最后电脑选的是不是『饭』,我们都知道这个模型是不靠谱的,因为『要』前面说了那么一大堆实际上是没有用到的。如果是3-Gram模型呢,会搜索『我要吃』后面最可能的词,感觉上比2-Gram靠谱了不少,但还是远远不够的。因为这句话最关键的信息『饿』,远在5个词之前!
现在读者可能会想,可以提升继续提升N的值呀,比如4-Gram、5-Gram…….。实际上,这个想法是没有实用性的。因为我们想处理任意长度的句子,N设为多少都不合适;另外,模型的大小和N的关系是指数级的,4-Gram模型就会占用海量的存储空间。
所以,我们的RNN就出场了,RNN理论上可以往前看(往后看)任意多个词。
基本递归神经网络
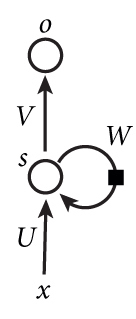
下图是一个简单的递归神经网络,它是由输入层、一个隐层和一个输出层组成的。
由图可知:
x:输入层的值U:输入层到隐层的权重参数s:隐层的值v:隐层到输出层的权重参数o:输出层的值W:递归神经网络的隐藏层的值s不仅仅取决于当前这次的输入x,还取决于上一次隐藏层的值s。权重参数W就是隐藏层上一次的值作为这一次的输入的权重。
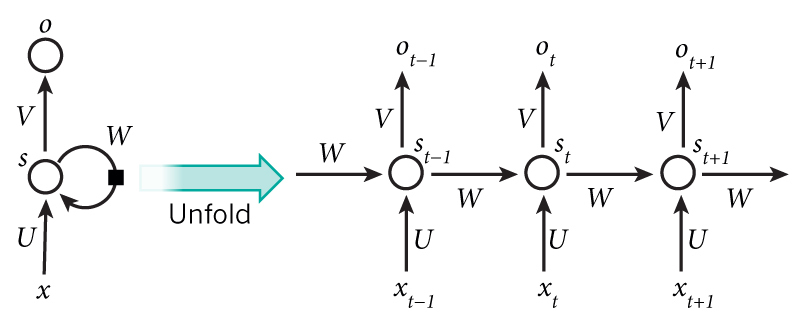
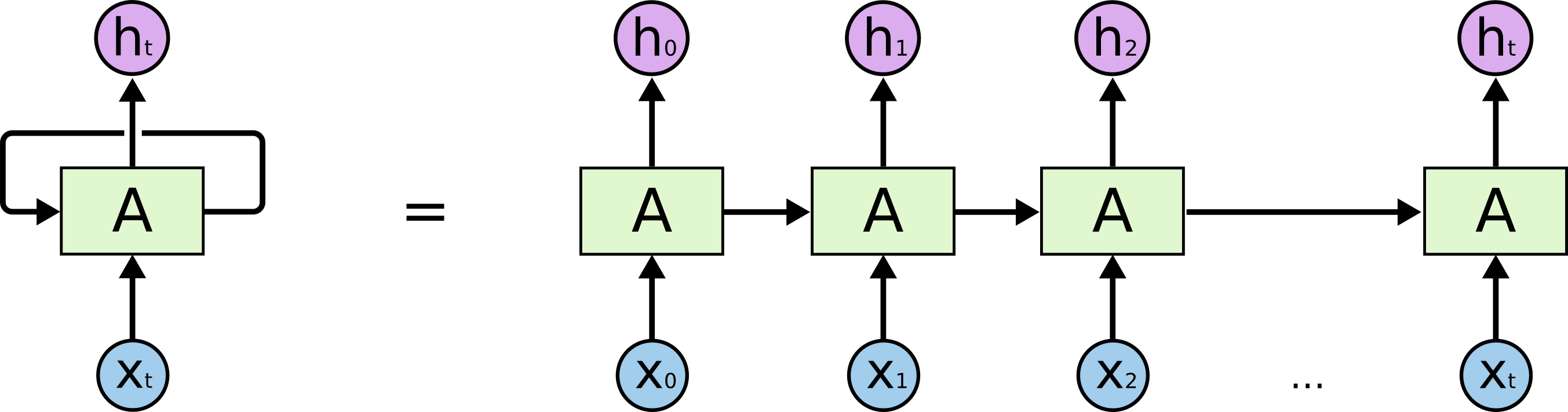
现在我们把上面的图展开,递归神经网络也可以画出这个结构:
从上图中,我们可以很直观的看出,这个网络在t时刻接收到$X_t$后,隐层的值是$S_t$,输出值是$O_t$。
关键点:$S_t$的值不仅仅取决于$X_t$,还取决于$S_{t-1}$(就是上一状态的隐层的值)。
公式:循环神经网络的计算公式:
$O_t=f(V \cdot S_t) \quad (1)$
输出层的计算公式,由于输出层是一个全连接层,所以说它每个节点都和隐层的节点相连。V是输出层的权重参数,f是激活函数。
$S_t=f(U \cdot X_t+W \cdot S_{t-1}) \quad (2)$
隐层的计算公式,它是一个循环层,U是输入x的权重参数,W是上一次的值$S_{t-1}$作为这一次输入的权重参数,f是激活函数。
总结:从上面的公式中,我们可以看出,循环层和全连接层的区别就是循环层多了一个权重参数w。
扩展:如果反复的把(1)式带入 (2)式:
${o}_t=f(V\cdot{S}_t) $
$ = V \cdot f(U \cdot X_t + W \cdot S_{t-1}) $
$= V \cdot f(U \cdot X_t+W \cdot f(U \cdot X_{t-1}+W \cdot S_{t-2}))$
$= V \cdot f(U \cdot X_t+W \cdot f(U \cdot X_{t-1}+W \cdot f(U \cdot X_{t-2}+W \cdot S_{t-3}))) $
$= V \cdot f(U \cdot X_t+W \cdot f(U \cdot X_{t-1}+W \cdot f(U \cdot X_{t-2}+W \cdot f(U \cdot X_{t-3}+…))))$
总结:从上面可以看出,递归神经网络的输出值$o_t$,是受前面几次输入值$X_t、X_{t-1}、X_{t-2}、X_{t-3}$…影响的,这也就是为什么递归神经网络可以往前看任意多个输入值的原因。
双向递归神经网络
介绍:它们只是两个堆叠在一起的RNN。然后基于两个RNN的隐藏状态计算输出。
对于语言模型来说,很多时候光看前面的词是不够的,比如下面这句话:
肚子好饿啊。我打算___一份外卖。可以想象,如果我们只是看横线前面的词,肚子好饿啊,我打算做饭,去吃饭还是什么什么的。这些都是无法确定的。但是如果我也先看横线后面的词【一份外卖】,那么横线上填【点】的概率就大多了。
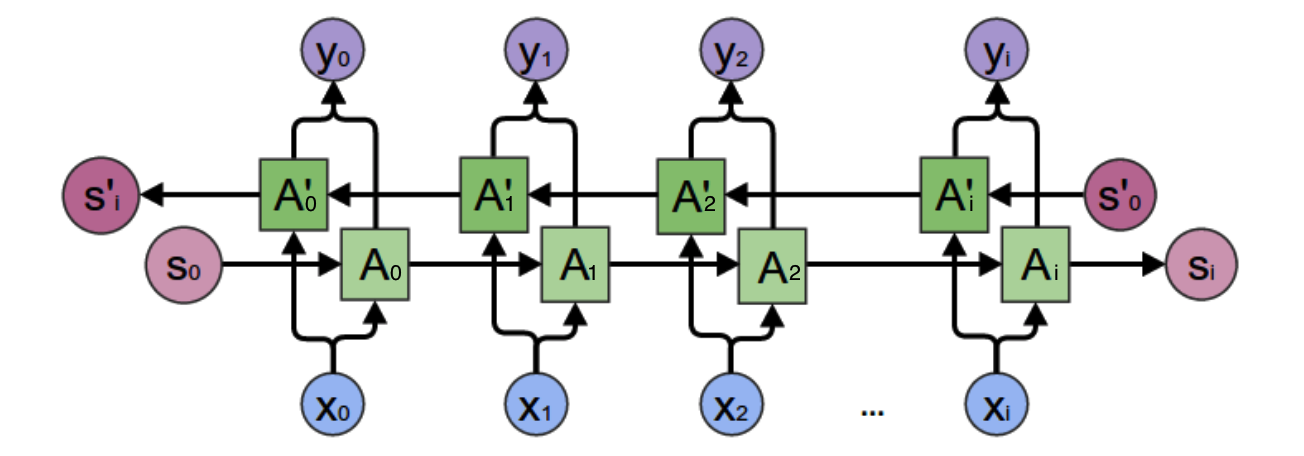
但是我们前面所讲的基本递归神经网络是无法解决这个问题的,这时我们就需要双向递归神经网络,如下图所示:
呃~~,有点复杂,我们先尝试分析一个特殊的场景,然后再总结规律。我们先看看上图的$y_2$的计算:
从上图可以看出,双向递归神经网络的隐层是需要保持两个值:
- $A$:参与正向计算
- $A’$:参与反向计算
所以$y_2$的值就取决于$A_2$和$A_2’$。计算方法:
$A_2$和$A_2’$则分别计算:
总结:
- 正向计算时:隐层的值$S_t$和$S_{t-1}$有关。
- 反向计算时:隐层的值$S_t’$和$S_{t-1}’$有关。
- 最终的输出取决于正向和反向计算的加和。
扩展:我们仿照(1)和(2)那种方式:
$o_t =f(V \cdot S_t+V’ \cdot S_t’) $
$S_t =f(U \cdot X_t+W \cdot S_{t-1}) $
$ S_t’=f(U’ \cdot X_t+W’ \cdot S_{t+1}’)$
注意:从上面三个公式我们可以看到,正向计算和反向计算不共享权重,也就是说U和U’、W和W’、V和V’都是不同的权重矩阵。
深度递归神经网络
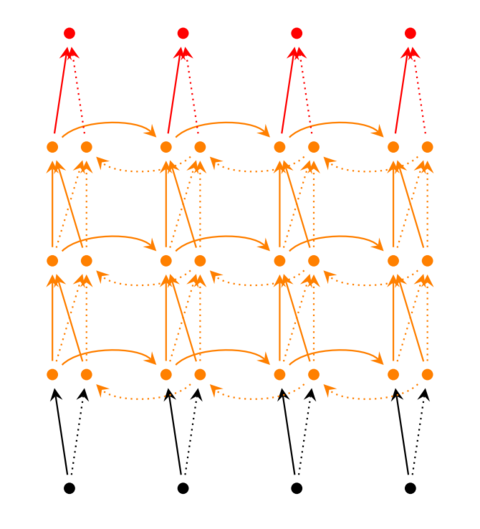
前面我们介绍的递归神经网络只有一个隐藏层,我们当然也可以堆叠两个以上的隐藏层,这样就得到了深度递归神经网络。如下图所示:
我们把第$i$个隐层的值表示为$S_t^{(i)}、S_t’^{(i)}$ ,则深度递归神经网络的计算方式就可以表示为:
${o}_t=f \cdot (V^{(i)} \cdot S_t^{(i)}+V’^{(i)} \cdot S_t’^{(i)})$
$S_t^{(i)}=f(U^{(i)}\cdot S_t^{(i-1)}+W^{(i)}\cdot S_{t-1})$
$S_t’^{(i)}=f(U’^{(i)}\cdot S_t’^{(i-1)}+W’^{(i)}\cdot S_{t+1}’)$
$…$
$S_t^{(1)}=f(U^{(1)} \cdot X_t+W^{(1)}\cdot S_{t-1})$
$S_t’^{(1)}=f(U’^{(1)}\cdot X_t+W’^{(1)}\cdot S_{t+1}’)$
总结
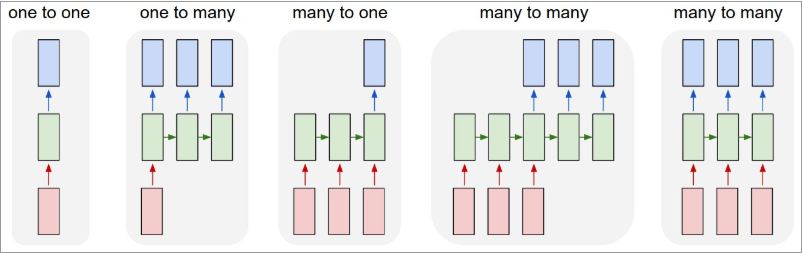
递归神经网络的形式很自由:不同的递归神经网络可以实现不同的功能
从上图我们可以总结出:
one to one:一个输入(单一标签)对应一个输出(单一标签)one to many:一个输入对应多个输出,即这个架构多用于图片的对象识别,即输入一个图片,输出一个文本序列。many to one: 多个输入对应一个输出,多用于文本分类或视频分类,即输入一段文本或视频片段,输出类别。many to many:这种结构广泛的用于机器翻译,输入一个文本,输出另一种语言的文本。many to many:这种广泛的用于序列标注。
在众多的深度学习网络中,RNN由于能够接收序列输入,也能得到序列输出,在自然语言处理中取得了巨大的成功,并得到广泛的应用。
本博客所有文章除特别声明外,均采用 CC BY-SA 3.0协议 。转载请注明出处!