机器学习-逻辑回归

逻辑回归

逻辑回归的概念

Logistic Regression 在《机器学习》-周志华一书中又叫对数几率回归。逻辑回归和多重线性回归实际上有很多的相同之处，除了它们的因变量（函数）不同外，其他的基本差不多，所以逻辑回归和线性回归又统属于广义线性模型（generalizedlinear model）。

广义线性模型的形式其实都差不多，不同的就是因变量（函数）的不同。

如果是连续的，就是多重线性回归
如果是二项分布，就是Logistic回归
如果是Poisson分布，就是Poisson分布
如果是负二项分布，就是负二项回归

Logistic回归的因变量可以是二分类的，也可以是多分类的，但是二分类的更为常用，也更加容易解释。所以实际中最常用的就是二分类的Logistic回归。

线性回归-Logistic回归

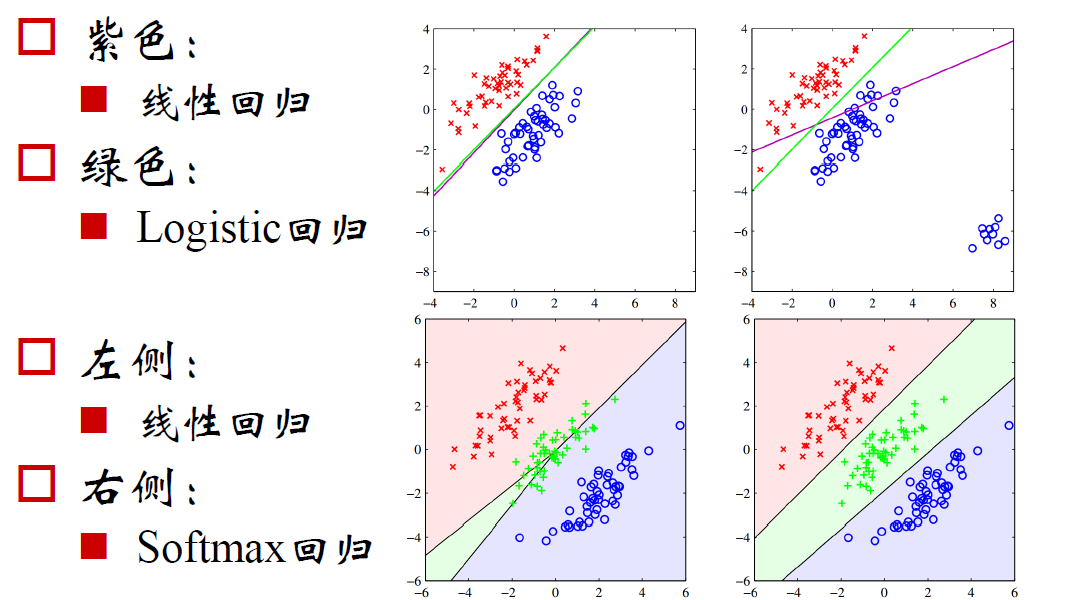
Logistic回归的主要用途：

寻找危险因素：寻找某一疾病的危险因素等；
预测：根据模型，预测在不同的自变量情况下，发生某病或某种情况的概率有多大；
判别：实际上跟预测有些类似，也是根据模型，判断某人属于某病或属于某种情况的概率有多大，也就是看一下这个人有多大的可能性是属于某病。

Logistic回归主要在流行病学中应用较多，比较常用的情形是探索某疾病的危险因素，根据危险因素预测某疾病发生的概率，等等。例如，想探讨胃癌发生的危险因素，可以选择两组人群，一组是胃癌组，一组是非胃癌组，两组人群肯定有不同的体征和生活方式等。这里的因变量就是是否胃癌，即“是”或“否”，自变量就可以包括很多了，例如年龄、性别、饮食习惯、幽门螺杆菌感染等。自变量既可以是连续的，也可以是分类的。

常规步骤

Regression问题的常规步骤为：

寻找h函数（即hypothesis）；
构造J函数（损失函数）；
想办法使得J函数最小并求得回归参数（θ）

构造预测函数（hypothesis）

Logistic回归虽然名字里带“回归”，但是它实际上是一种分类方法，主要用于两分类问题（即输出只有两种，分别代表两个类别），所以利用了Logistic函数（或称为Sigmoid函数），函数形式为：

$g(z)=\frac{1}{1+e^{-z}}$

为了方便后面使用我们求出$g(z)$的导数：

$g^{‘}(z)=\frac1{1+e^{-z} } \cdot (1- \frac1{1+e^{-z} })=g(z)(1-g(z))$

Sigmoid 函数在有个很漂亮的“S”形，如下图所示

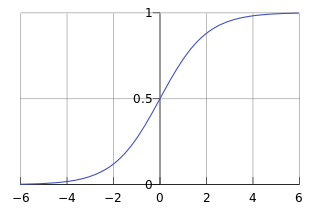
构建预测函数

决策边界又分为线性的决策边界和非线性的决策边界

线性的决策边界：

非线性的决策边界：

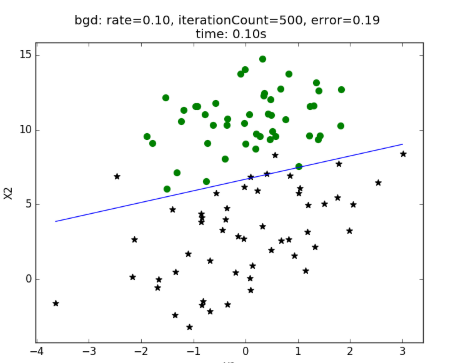
对于线性边界的情况，边界形式如下：

$\theta_0+\theta_1x_1+\cdot \cdot \cdot + \theta_nx_n=\sum_{i=1}^n \theta_ix_i = \theta^Tx$

构建的预测函数为：

$h_\theta(x)=g(\theta^Tx)=\frac1{1+e^{-\theta^Tx}}$

构建损失函数

由于是二项分布，函数$h_ \theta(x)$的值就有特殊的含义，它所表示的是结果取1的概率，因此对于输入x的分类结果就判别为类别1和类别0的概率分别为：

$P(y=1|x;\theta)=h_\theta(x) \\ P(y=0|x;\theta)=1-h_\theta(x)$

所以：

$P(y|x;\theta) = {h_\theta(x) }^y{(1-h_\theta(x)) }^{1-y}$

构建似然函数

$L(\theta)=\prod_{i=1}^n P(y_i|x_i;\theta) =\prod_{i=1}^n {h_\theta(x_i) }^{y_i}{(1-h_\theta(x_i)) }^{1-y_i}$

对数似然函数

$l(\theta)=logL(\theta)=\sum_{i=1}^n(y_ilogh_\theta(x_i)+(1-y_i)log(1-h_\theta(x_i)))$

最大似然估计就是求使$l(\theta)$取最大值时的θ，其实这里可以使用梯度上升法求解，求得的θ就是要求的最佳参数。

梯度下降法求的最小值

θ更新过程：

$\theta_j :=\theta_j-a(\frac{\partial l(\theta)}{\partial \theta_j})$

对$\theta$求偏导

$\frac{\partial l(\theta)}{\partial \theta_j}=\frac{\partial g(\theta^Tx)}{\partial \theta_j}(\frac{y}{g(\theta^Tx)}-\frac{1-y}{g(\theta^Tx)})$

$=g(\theta^Tx)(1-g(\theta^Tx)) \frac{\partial\theta^Tx}{\partial \theta_j}(\frac{y}{g(\theta^Tx)}-\frac{1-y}{g(\theta^Tx)})$

$=(y(1-g(\theta^Tx))-(1-y)g(\theta^Tx))x_j$

$=(y-h_\theta(x))x_j$

θ更新过程就可以写为：

$\theta_j :=\theta_j-a\sum_{i=1}^n (y_i-h_\theta(x_i))x_i^j$

但是在在Andrew Ng的课程中将 $J(\theta)$取为下式，即：

$J(\theta)=-\frac{1}{m}l(\theta)$

因为乘了一个负的系数-1/m，所以取 $J(\theta)$最小值时的θ为要求的最佳参数。

$\frac{\partial l(\theta)}{\partial \theta_j}=\frac 1 m \sum_{i=1}^n(h_\theta(x_i)-y_i)x_i^j$

相应的$\theta$:

$\theta_j :=\theta_j-a \frac 1 m \sum_{i=1}^n (h_\theta(x_i)-y_i)x_i^j$

向量化（Vectorization ）

Vectorization是使用矩阵计算来代替for循环，以简化计算过程，提高效率。

如上式，Σ(…)是一个求和的过程，显然需要一个for语句循环m次，所以根本没有完全的实现vectorization。

下面介绍向量化的过程：

约定训练数据的矩阵形式如下，x的每一行为一条训练样本，而每一列为不同的特称取值：

g(A)的参数A为一列向量，所以实现g函数时要支持列向量作为参数，并返回列向量。由上式可知 $h_\theta(x)-y$可以由$g(A)-y$一次求得

θ更新过程可以改为

$\theta_j :=\theta_j-a \frac 1 m \sum_{i=1}^n (h_\theta(x_i)-y_i)x_i^j=\theta_j-a \frac 1 m \sum_{i=1}^n e_ix_i^j=\theta_j-a \frac1 m x^TE$

综上所述，Vectorization后θ更新的步骤如下：

求:$A=x \cdot \theta$
求$E=g(A)-y$
求$\theta:=\theta-ax^TE$

正则化Regularization

同样逻辑回归也有欠拟合、适合拟合、过拟合问题

对于线性回归或逻辑回归的损失函数构成的模型，可能会有些权重很大，有些权重很小，导致过拟合（就是过分拟合了训练数据），使得模型的复杂度提高，泛化能力较差（对未知数据的预测能力）。

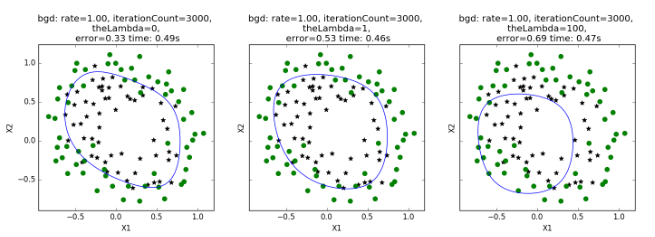
下面左图即为欠拟合，中图为合适的拟合，右图为过拟合。

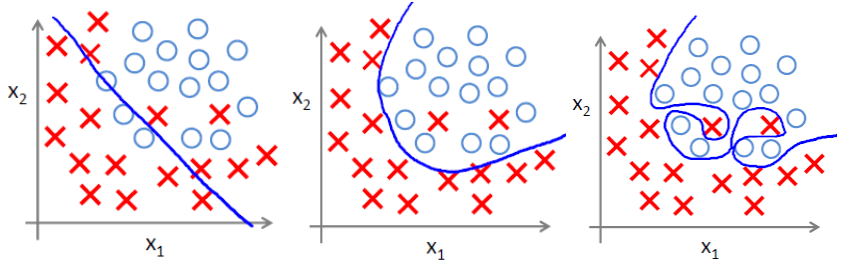
过拟合问题往往源自过多的特征。

解决方法

1）减少特征数量（减少特征会失去一些信息，即使特征选的很好）

可用人工选择要保留的特征；
模型选择算法；

2）正则化（特征较多时比较有效）

保留所有特征，但减少θ的大小

正则化方法

正则化是结构风险最小化策略的实现，是在经验风险上加一个正则化项或惩罚项。正则化项一般是模型复杂度的单调递增函数，模型越复杂，正则化项就越大。

在线性回归算法的正则化问题,正则项可以取不同的形式，在回归问题中取平方损失，就是参数的L2范数，也可以取L1范数。取平方损失时，模型的损失函数变为：

$J(\theta)=\frac1{2m}\sum_{i=1}^{n}(h_\theta(x_i)-y_i)^2+\lambda\sum_{j=1}^n \theta_j^2$

lambda是正则项系数：

如果它的值很大，说明对模型的复杂度惩罚大，对拟合数据的损失惩罚小，这样它就不会过分拟合数据，在训练数据上的偏差较大，在未知数据上的方差较小，但是可能出现欠拟合的现象；
如果它的值很小，说明比较注重对训练数据的拟合，在训练数据上的偏差会小，但是可能会导致过拟合。

正则化后的梯度下降算法θ的更新变为：

$\theta_j :=\theta_j-a \frac 1 m \sum_{i=1}^n (h_\theta(x_i)-y_i)x_i^j - \frac \lambda m \theta_j$

其他优化算法

Conjugate gradient method(共轭梯度法)
Quasi-Newton method(拟牛顿法)
BFGS method(局部优化法)
L-BFGS(Limited-memory BFGS)（有限内存局部优化法）

后二者由拟牛顿法引申出来，与梯度下降算法相比，这些算法的优点是：

第一，不需要手动的选择步长；
第二，通常比梯度下降算法快；

但是缺点是更复杂。

多类分类问题

多类分类问题中,我们的训练集中有多个类(>2),我们无法仅仅用一个二元变量(0或1)来做判断依据。例如我们要预测天气情况分四种类型:晴天、多云、下雨或下雪。下面是一个多类分类问题可能的情况:

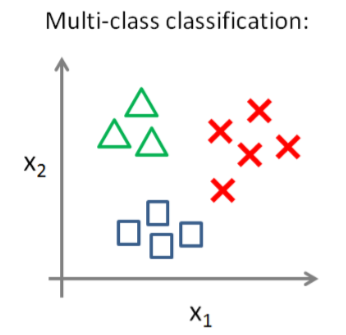
一种解决这类问题的途径是采用一对多(One-vs-All)方法（可以将其看做成二类分类问题：保留其中的一类，剩下的作为另一类）。在一对多方法中,我们将多类分类问题转化成二元分类问题。为了能实现这样的转变,我们将多个类中的一个类标记为正向类(y=1),然后将其他所有类都标记为负向类,这个模型记作：

$h_\theta^{(1)}(x)$

接着,类似地第我们选择另一个类标记为正向类(y=2),再将其它类都标记为负向类,将这个模型记作,

$h_\theta^{(2)}(x)$

依此类推。最后我们得到一系列的模型简记为:

$h_\theta^{(i)}(x)=p(y=i|x;\theta)$

其中 i = 1,2,3,…,k步骤可以记作下图：

最后,在我们需要做预测时,我们将所有的分类机都运行一遍,然后对每一个输入变量,都选择最高可能性的输出变量。