线性回归–$y=wx+b$

回归，统计学术语，表示变量之间的某种数量依存关系，并由此引出回归方程，回归系数。

线性回归（Linear Regression）

数理统计中回归分析，用来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，其表达形式为$y = wx+e$，e为误差服从均值为0的正态分布，其中只有一个自变量的情况称为简单回归，多个自变量的情况叫多元回归。

注意，统计学中的回归并如线性回归非与严格直线函数完全能拟合，所以我们统计中称之为回归用以与其直线函数区别。

我们先来看下这个图

这个是近期比较火的现金贷产品的贷款额度。这个表格表示的是可贷款的金额与 工资和 房屋面积之间的关系，其中 工资 和 房屋面积 为 特征，可贷款金额为目标函数值。 那么根据线性函数可得到以下公式。

$h_\theta(x)=\theta_{1}x_{1}+\theta_{2}x_{2} $

上面的这个式子是当一个模型只有两个特征$(x_1,x_2)$的时候的线性回归式子。 正常情况下，现金贷中可贷款的额度和用户的很多特征相关联，并不只是简单的这两个特征。所以我们需要把这个式子进行通用化。 假如有n个特征的话，那么式子就会变成下面的样子

$h_\theta(x)=\theta_{1}x_{1}+\theta_{2}x_{2} + \cdot \cdot \cdot \cdot \cdot+\theta_{n}x_{n} = \sum_{i=1}^{n}\theta_{i}x_{i}$

利用矩阵的知识对线性公式进行整合。

因为机器学习中基本上都是用矩阵的方式来表示参数的，也就是说我们需要把这个多项求和的式子用矩阵的方式表达出来，这样才方便后续的计算。

$\theta_{i \times 1} = [\theta_1,\theta_2,\cdot\cdot\cdot\theta_i,]$

$X_{i\times1}=[x_1,x_2,\cdot \cdot \cdot x_i]$

把上述线性函数写成矩阵相乘的形式

$\theta^TX=\begin{bmatrix} \theta_1 \\ \theta_2 \\ \cdot \\ \cdot \\ \cdot \\ \theta_i \end{bmatrix} \cdot [x_1,x_2,\cdot \cdot \cdot x_i] = \sum_{i=1}^{n}\theta_{i}x_{i} $

我们把权重参数和特征参数，都看成是1行n列的矩阵(或者是行向量)。那么就可以根据矩阵乘法的相关知识，把上述多项求和的式子，转换成矩阵的乘法的表达式。 由此我们就把多项求和化简称了 。

$h_\theta(x)=\theta^TX$

误差项的分析

原式:$$y =wx+b$$ 其中$b$就是我们所说的偏移量，或者叫误差项。

我们再看看下面这个图：

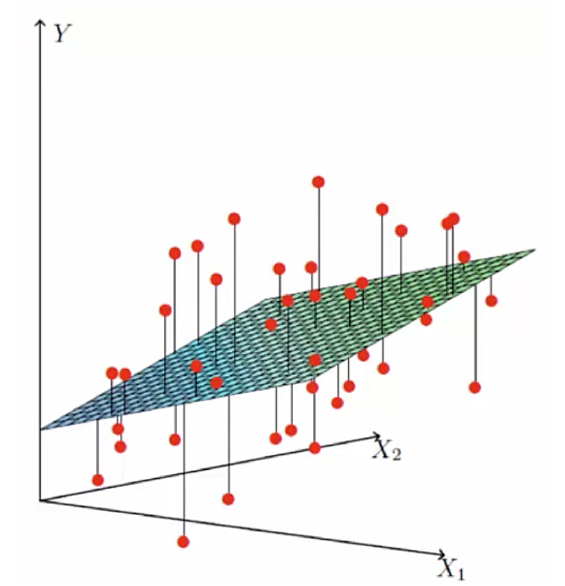
图中的横坐标$x_1$ 和 X$x)_2$分别代表着 两个特征(工资、房屋平米) 。纵坐标Y代表目标(可贷款的额度)。其中红点代表的就是实际的目标值(每个人可贷款的额度).而平面上和红点竖向相交的点代表着我们根据线性回归模型得到的点。也就是说实际得到的钱和预估的钱之间是有一定误差的，这个就是误差项。 因为误差项是真实值和误差值之间的一个差距。那么肯定我们希望误差项越小越好。

然后我们对应整理成线性回归函数：

$h_\theta(x)=\theta^Tx+\varepsilon$

我们根据实际情况，假设认为这个误差项是满足以下几个条件的。

1. 误差$\varepsilon_{(i)}$是独立。
2. 具有相同的分布。
3. 服从均值为0方差为$\theta^2$的高斯分布。

然我们回到刚开始的现金贷产品的贷款额度问题上面

1.独立：张三和李四一起使用这款产品，可贷款额互不影响

2.同分布：张三和李四是使用的是同一款产品

3.高斯分布：绝大多数的情况下，在一个的空间内浮动不大

似然函数的理解

由前面两步，我们已经把线性回归模型，推导成下面的这个式子了

$y_{(i)}=\theta^Tx_i+\varepsilon_i$

我们已经知道误差项是符合高斯分布的，所以误差项的概率值：

$P(\varepsilon_i)=\frac{1}{\sqrt{2\pi}\sigma}e^{-(\frac{(\varepsilon_i)^2}{2\sigma^2})}$

然后把误差值带入式子中:

$P(y_i|x_i,\theta)=\frac{1}{\sqrt{2\pi}\sigma}e^{-(\frac{(y_i-\theta^Tx_i)^2}{2\sigma^2})}$

由于是误差值，所以是越小越好，所以我们接下来就是讨论什么样的特征值和特征组合能够让误差值最小，现在就要看似然函数的作用了，似然函数的作用就是要根据样本求什么样的参数和特征的组成能够接近真实值，所以越接近真实值则误差就越小。

引入似然函数(似然函数就是求能让真实值和预测值相等的那个参数的 )：

$L(\theta) = \prod_{i=1}^{N} P(y_i|x_i,\theta)=\prod_{i=1}^{N}\frac{1}{\sqrt{2\pi}\sigma}e^{-(\frac{(y_i-\theta^Tx_i)^2}{2\sigma^2})}$

$\prod$表示各元素相乘的结果

上面的式子是多个参数的乘积的形式，很难进行计算，所以我们又采用了对数的一个小技巧，把多个数相乘，转化成多个数相加的形式。

因为对数的性质

$logA\cdot B = logA+logB$

根据上面的这种换算关系，我们就把似然函数的式子换算成下面的这个。 (因为似然函数是越大越好，似然函数的值和对数似然函数的值是成正比的，对值求对数，并不会影响到最后求极限的值。所以才敢进行对数处理。)

$l(\theta) = logL(\theta) = log\prod_{i=1}^{N}\frac{1}{\sqrt{2\pi}\sigma}e^{-(\frac{(y_i-\theta^Tx_i)^2}{2\sigma^2})}$

对上式进行整理：

$l(\theta) = logL(\theta) = \sum_{i=1}^{N}log\frac{1}{\sqrt{2\pi}\sigma}e^{-(\frac{(y_i-\theta^Tx_i)^2}{2\sigma^2})}$

$= \sum_{i=1}^{N}(log\frac{1}{\sqrt{2\pi}\sigma}+loge^{-(\frac{(y_i-\theta^Tx_i)^2}{2\sigma^2})})$

$= Nlog\frac{1}{\sqrt{2\pi}\sigma}-\frac{1}{2\sigma^2}\sum_{i=1}^{N}(y_i-\theta^Tx_i)^2 $

因为：

$Nlog\frac{1}{\sqrt{2\pi}\sigma}$ 是一个定值

似然函数是要越大越好

所以：

$-\frac{1}{2\sigma^2}(y_i-\theta^Tx_i)^2$越大越好

再因为：

$-\frac{1}{2\sigma^2}$也为定值

最终：

$l(\theta) = \sum_{i=1}^{N}(y_i-\theta^Tx_i)^2$

$\sum_{i=1}^{N}(y_i-\theta^Tx_i)^2$越小越好——最小二乘法（损失函数）

最小二乘法

上述代价函数中使用的均方误差，其实对应了我们常用的欧几里得的距离（欧式距离，Euclidean Distance）, 基于均方误差最小化进行模型求解的方法称为“最小二乘法”（least square method），即通过最小化误差的平方和寻找数据的最佳函数匹配；

当函数子变量为一维时，最小二乘法就蜕变成寻找一条直线；

然后我们把得到的损失函数推广到n维，转换成矩阵形式（参考前面利用矩阵的知识对线性公式进行整合）：

$J(\theta)=\sum_{i=1}^{N}(y_i-\theta^Tx_i)^2$ 损失函数

其对应的均方误差表示为如下矩阵

$J(\theta) = {(y-X\theta)^T(y-X\theta)}$

其中X：

$X=\begin{bmatrix} 1 && x_1^T \\ 1 && x_2^T \\ \cdot \\ \cdot \\ \cdot \\ 1 && x_N^T \end{bmatrix} =\begin{bmatrix} 1 && x_{11} && x_{12} && \cdot \cdot \cdot x_{1n} \\ 1 && x_{21} && x_{22} && \cdot \cdot \cdot x_{2n} \\ \cdot \\ \cdot \\ \cdot \\ 1&& x_{m1} && x_{m2} && \cdot \cdot \cdot x_{mn} \end{bmatrix} $

对$\theta$求导

$J(\theta) = {(y-X\theta)^T(y-X\theta)}=y^Ty-y^Tx\theta-\theta^Tx^Ty+\theta^Tx^Tx\theta$

$\frac{\partial J(\theta)}{\partial(\theta)} = \frac{\partial y^Ty}{\partial(\theta)} - \frac{\partial y^Tx\theta}{\partial(\theta)} - \frac{\partial \theta^Tx^Ty}{\partial(\theta)} + \frac{\partial \theta^Tx^Tx\theta}{\partial(\theta)} $

$\frac{\partial J(\theta)}{\partial(\theta)} = 0-x^Ty-x^Ty+2x^Tx\theta$

$\frac{\partial J(\theta)}{\partial(\theta)} =2x^T(x\theta-y)$

根据导数的性质，该值在导数为0时为最小

所以：根据微积分定理，令上式等于零，可以得到 θ 最优的闭式解。当

$2(x^Ty-x^Tx\theta)=0$时取得最小

矩阵求导的知识：

最终：$\theta = (x^Tx)^{-1}x^Ty$

X和Y都是已知的，那么得到了最终的参数值。

那我们来看看数学原理

微积分角度来讲，最小二乘法是采用非迭代法，针对代价函数求导数而得出全局极值，进而对所给定参数进行估算。

计算数学角度来讲，最小二乘法的本质上是一个线性优化问题，试图找到一个最优解。

线性代数角度来讲，最小二乘法是求解线性方程组，当方程个数大于未知量个数，其方程本身 无解，而最小二乘法则试图找到最优残差。

几何角度来讲，最小二乘法中的几何意义是高维空间中的一个向量在低维子空间的投影。

概率论角度来讲，如果数据的观测误差是/或者满足高斯分布，则最小二乘解就是使得观测数据出现概率最大的解，即最大似然估计-Maximum Likelihood Estimate，MLE（利用已知的样本结果，反推最有可能（最大概率）导致这样结果的参数值）。