机器学习-聚类

无监督学习

无监督学习是一种机器学习方法，用于发现数据中的模式。输入无监督算法的数据都没有标签，也就是只为算法提供了输入变量$(X)$而没有对应的输出变量。在无监督学习中，算法需要自行寻找数据中的结构。

无监督学习问题可以有以下三种类型：

关联：发现目录中项目共现的概率。其广泛应用于“购物车分析”。例如，如果一个顾客购买了火腿，他会有80% 的概率也购买鸡蛋。
聚类：将样本分组，这样，同一聚类中的物体与来自另一聚类的物体相比，相互之间会更加类似。
降维：降维指减少一个数据集的变量数量，同时保证还能传达重要信息。降维可以通过特征抽取方法和特征选择方法完成。特征选择方法会选择初始变量的子集。特征抽取方法执行从高维度空间到低维度空间的数据转换。例如，PCA算法就是一种特征抽取方式。

聚类的概念

聚类是一种无监督机器学习方法，它基于数据的内部结构寻找观察样本的自然族群（即集群），常用于新闻分类、推荐系统等。聚类的特点是训练数据没有标注，通常使用数据可视化评价结果。

聚类分析仅根据在数据中发现的描述对象及其关系的信息，将数据对象分组。其目标是，组内的对象相互之间是相似的（相关的），而不同组中的对象是不同的（不相关的）。组内的相似性（同质性）越大，组间差别越大，聚类就越好。

聚类的方法

聚类的常用方法包括

划分聚类法，K均值:是基于原型的、划分的聚类技术。它试图发现用户指定个数K的簇（由质心代表）。
层次聚类。凝聚的层次聚类：开始，每个点作为一个单点簇；然后，重复地合并两个最靠近的簇，直到产生单个的、包含所有点的簇。
基于密度的聚类， DBSCAN是一种产生划分聚类的基于密度的聚类算法，簇的个数由算法自动地确定。低密度区域中的点被视为噪声而忽略，因此DBSCAN不产生完全聚类。

常用的聚类数据集

常用的聚类数据集包括

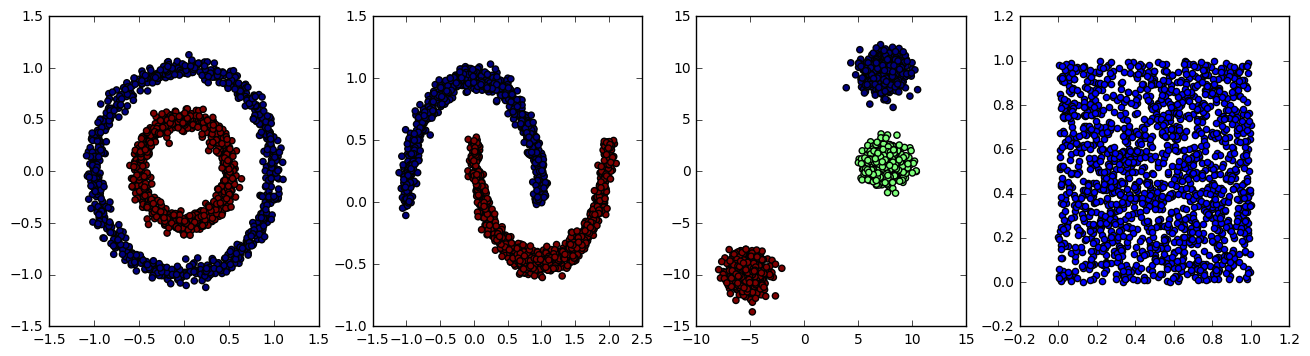
scikit-learn blob: 简单聚类
scikit-learn circle: 非线性可分数据集
scikit-learn moon: 更复杂的数据集

聚类的性能度量

我们希望聚类结果的“簇内相似度”高且“簇间相似度”低。

其性能度量大致有两类：

一类是将聚类结果与某个“参考模型”进行比较。称为“外部指标”。

一类是直接考查聚类结果而不利于任何参考模型。称为“内部指标”。

外部指标

对数据集$D={x_1,x_2,…,x_m}$,假定通过聚类给出额簇划分为$C=C_1,C_2,…,C_k$,参考模型给出的簇划分为$C’=C_1^T,C_2^T,…,C_s^T$。相应的，令λ与$λ^T$分别表示与C和$C^T$对应的簇标记向量。注意的是，参考模型给出的划分类别数量不一定等于通过聚类得到的数量。

样本两两配对：

$a=\mid SS \mid ,SS={(x_i,x_j)\mid \lambda_i = \lambda_j,\lambda_i^T=\lambda_j^T,i<j}$
$b=\mid SS \mid ,SD={(x_i,x_j)\mid \lambda_i = \lambda_j,\lambda_i^T\neq \lambda_j^T,i<j}$
$c=\mid SS \mid ,DS={(x_i,x_j)\mid \lambda_i \neq \lambda_j,\lambda_i^T=\lambda_j^T,i<j}$
$d=\mid SS \mid ,DD={(x_i,x_j)\mid \lambda_i \neq \lambda_j,\lambda_i^T \neq \lambda_j^T,i<j}$

集合SS包含了C中隶属于相同簇且在$C’$中也隶属于相同簇的样本对，集合SD包含了在C中隶属于相同簇但在$C^T$中隶属于不同簇的样本对 .

Jaccard系数：$JC=\frac{a}{a+b+c}$
FM指数： $FMI=\sqrt{\frac{a}{a+b}\frac{a}{a+c}}$
Rand指数： $RI=\frac{2(a+d)}{m(m-1)}$

上述性能度量的结果值均在[0,1]区间，值越大越好。

内部指标

考虑聚类结果的簇划分$C=C_1,C_2,…,C_k$，定义

$avg(C)=\frac{2}{\mid C \mid(\mid C \mid -1)}\sum_{1 \leq i < j \leq \mid C \mid}dist(x_i,x_j)$
$diam(C)=\max_{1 \leq i <j \leq \mid C \mid}dist(x_i,x_j)$
$d_\min(C_i,C_j)=\min_{x_i \in C_i , x_j \in C_j} dist(x_i,x_j)$
$d_cen(C_i,C_j)=dist(\mu_i,\mu_j)$

我们在上面的式子中，dist是计算两个样本之间的距离，$u$代表簇的中心点$\mu=\frac{\sum_{1 \leq i \leq \mid C \mid x_i}}{\mid C \mid}$ ，avg(C)与簇内样本间的平均距离，diam(C)对应与簇C内样本间的最远距离，$d_min(C_i,Cj)对应与簇i和簇j最近样本间的距离；对应与簇i和簇j最近样本间的距离；d{cen}(C_i,C_j)$对应与簇i和j中心点间的距离。

基于上面的指标，推出下面几个内部指标：

$DBI=\frac{1}{k}\sum\limits_{i=1}^k\max\limits_{j \neq i}(\frac{avg(C_i)+avg(C_j)}{d_{cen}(\mu_i,\mu_j)})$
$DI=\min\limits_{1 \leq i \leq k}{ \min\limits_{j \neq i}(\frac{d_{min}(C_i,C_j)}{\max_{1\leq l \leq k diam(C_l)}}) }$

显然，DBI的值越小越好，DI值越大越好

相似度/距离度量

“距离度量”需满足一些基本性质，如非负性、同一性、对称性和直递性。最常用的是闵可夫斯基距离、欧氏距离和曼哈顿距离（后两者其实都是闵可夫斯基距离的特例）。

闵可夫斯基距离只可用于有序属性，对无序属性可采用VDM（Value Difference Metric）。

计算方法总结：

闵可夫斯基距离Minkowski/欧式距离：$dist(X,Y)=(\sum_{i=1}^n|x_i-y_i|^p)^\frac1p$
杰卡德相似系数(Jaccard): $J(A,B)=\frac{|A\cap B|}{|A\cup B|}$
余弦相似度(cosine similarity):$cos(\theta)=\frac{a^Tb}{|a|\cdot |b|}$
Pearson相似系数：$\rho_{xy}=\frac{cov(X,Y)}{\sigma_X\sigma_Y}=\frac{E[(X-u_X)(Y-u_Y)]}{\sigma_X\sigma_Y}=\frac{\sum_{i=1}^n (X_i-u_X)(Y_i-u_Y) }{\sqrt{\sum_{i=1}^n(X_i-u_X)^2} \sqrt{\sum_{i=1}^n(Y_i-u_Y)^2}}$
相对熵（K-L距离）：$D(P||q)=\sum_xp(x)log\frac{p(x)}{q(x)}=E_{p(x)}log\frac{p(x)}{q(x)}$
Hellinger距离：$D_a(p||q)=\frac{2}{1-a^2}(1-\int (p(x)^\frac{1+a}{2}\cdot q(x)^\frac{1-a}{2}dx$

聚类的基本思想

给定一个有N个对象的数据集，构造数据的K个簇，$k\le n$,满足下列条件：

每一个簇至少包含一个对象
每一个对象属于且仅属于一个簇
将满足上述条件的K个簇称作一个合理的划分

基本思想：对于给定的类别数目K，首先给出初始划分，通过迭代改变样本和簇的隶属关系，使得每一次改进之后的划分方案都比前一次好。

原型聚类

原型聚类亦称“基于原型的聚类”，假设聚类结构能通过一组原型（原型是指样本空间中具有代表性的点）刻画。

常用的方法包括

k均值算法
学习向量化
高斯混合聚类（基于概率模型）

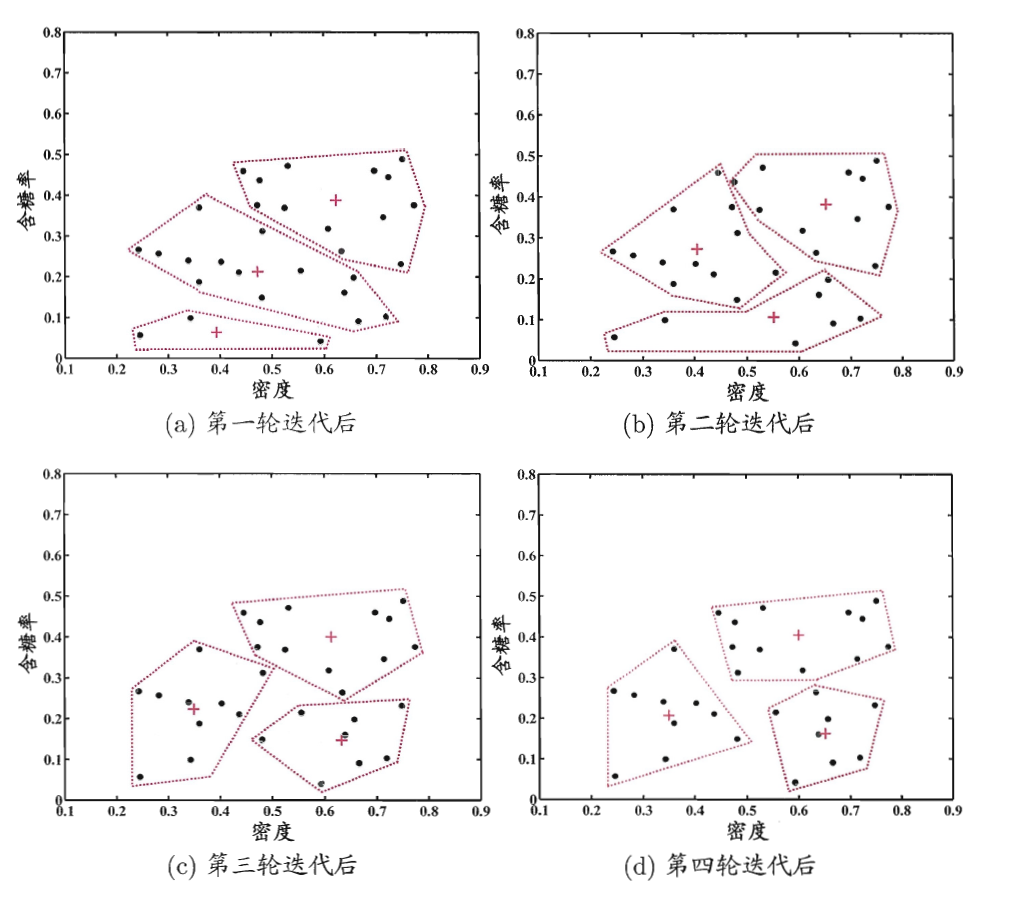
K-Means 聚类

K-Means算法的基本思想是初始随机给定K个簇中心，按照最邻近原则把待分类样本点分到各个簇。然后按平均法重新计算各个簇的质心(这个点可以不是样本点)，从而确定新的簇心。一直迭代，直到簇心的移动距离小于某个给定的值。

K-Means聚类算法步骤：

(1)选择K个初始质心，其中K是用户指定的参数，即所期望的簇的个数。

(2)每个点指派到最近的质心，而指派到一个质心的点集为一个簇。

(3)根据指派到簇的点，更新每个簇的质心。

(4)重复指派和更新步骤，直到簇不发生变化，或等价地，直到质心不发生变化。

K均值算法

k均值常用的邻近度，质心和目标函数的选择：

邻近度函数：曼哈顿距离。质心：中位数。目标函数：最小化对象到其簇质心的距离和。

邻近度函数：平方欧几里德距离。质心：均值。目标函数：最小化对象到其簇质心的距离的平方和。

邻近度函数：余弦。质心：均值。最大化对象与其质心的余弦相似度和。

邻近度函数：Bregman散度。质心：均值。目标函数：最小化对象到其簇质心的Bregman散度和。

由于基本K均值算法采取随机地选取初始质心的办法，导致最后形成的簇的质量常常很糟糕。在此基础上引出了基本K均值算法的扩充：二分K均值算法。二分K均值算法不太受初始化问题的影响。

二分K均值算法

把所有数据作为一个cluster加入cluster list
repeat
从cluster list中挑选出一个SSE最大的cluster来进行划分
for i=1 to预设的循环次数
用基本K均值算法把挑选出来的cluster划分成两个子cluster
计算两个子cluster的SSE和。
end for
把for循环中SSE和最小的那两个子cluster加入cluster list
until cluster list拥有K个cluster

除此以外，每次划分不止执行一次基本K均值算法，而是预先设置一个ITER值，然后对这个cluster进行ITER次执行基本K均值运算。因为基本K均值每次一开始都是随机选K个质心来执行，所以i一般来说ITER次执行基本K均值，每次都会得到不同的两个cluster。那么应该选哪对cluster来作为划分以后的cluster呢？答案就是在每次循环中，每次都计算当次基本K均值划分出来的两个cluster的SSE和，最后就选SSE和最小的那对cluster作为划分以后的cluster。

学习向量化

与k均值算法类似，“学习向量量化”（Learning Vector Quantization，简称LVQ）也是试图找到一组原型向量来刻画聚类结构，但与一般的聚类算法不同的是，LVQ假设数据样本带有类别标记，学习过程用样本的这些监督信息来辅助聚类。

学习向量化算法

高斯混合模型

高斯混合聚类使用了一个很流行的算法：GMM(Gaussian Mixture Model)。高斯混合聚类与k均值聚类类似，但是采用了概率模型来表达聚类原型。每个高斯模型（Gaussian Model）就代表了一个簇（类）。GMM是单一高斯概率密度函数的延伸，能够平滑地近似任意形状的密度分布。在高斯混合聚类中，每个GMM会由k个高斯模型分布组成，每个高斯模型被称为一个component，这些component线性加乘在一起就组成了GMM的。

简单地来说，k-Means的结果是每个数据点没分配到其中某一个cluster,而GMM则给出的是这个数据点被分配到每个cluster的概率，又称为soft assignment。

高斯混合模型聚类算法

层次聚类

层次聚类（hierarchical clustering）试图在不同层次对数据集进行划分，从而形成树形的聚类结构。数据集的划分可采用“自底向上”的聚合策略，也可采用“自顶向下”的分拆策略。典型的AGNES是一种采用自底向上聚合策略的层次聚类算法。它先将数据集中的每个样本看作一个初始聚类簇，然后在算法运行的每一步中找出距离最近的两个聚类簇进行合并，该过程不断重复，直至达到预设的聚类簇个数。

有两种产生层次聚类的基本方法：

凝聚的。从点作为个体簇开始，每一步合并两个最接近的簇。这需要定义簇的临近性概念。凝聚层次聚类技术最常见。
分裂的。从包含所有点的某个簇开始，每一步分裂一个簇，直到仅剩下单点簇。在这种情况下，我们需要确定每一步分裂哪个簇，以及如何分裂。

层次聚类算法

基本凝聚层次聚类算法：

如果需要，计算临近度矩阵
repeat
合并最接近的两个簇
更新临近度矩阵，以反映新的簇与原来的簇之间的临近性。
until 仅剩下一个簇

簇之间的临近性有3种定义方式：

MIN（单链）。不同簇中的两个最近的点之间的距离作为临近度。
MAX（全链）。不同簇中的两个最远的点之间的距离作为临近度。
GROUP（组平均）。取自不同簇的所有点对距离的平均值作为临近度。

注意：

簇与簇合并的原则永远是dist最小。
但在计算dist值的时候，可以采用MIN, MAX, GROUP AVG 3中方式得出dist的值。

密度聚类

密度聚类亦称“基于密度的聚类”，假设聚类结构能通过样本分布的紧密程度确定。典型的代表算法为DBSCAN算法，它基于一组“领域”（neighborhood）参数来刻画样本分布的紧密程度。

DBSCAN将“簇”定义为：由密度可达关系导出的最大的密度相连样本集合。

DBSCAN算法

基于密度的聚类寻找被低密度区域分离的高密度区域。DBSCAN是一种简单、有效的基于密度的聚类算法。

DBSCAN算法：

将所有点标记为核心点、边界点或噪声点。
删除噪声点。
为距离在Eps之内的所有核心点之间连线。
每组连通的核心点形成一个簇。
将每个边界点指派到一个与之关联的核心点的簇中。

DBSCAN算法阐释：

算法需要用户输入2个参数：半径Eps; 最小（少）点值MinPts。
确定Eps和MinPts需要用到K-距离的概念。K-距离就是“到第K近的点的距离”，按经验一般取值为4。并且，一般取K的值为MinPts参数的值。
首先计算每个点到所有其余点的欧式距离，升序排序后，选出每个点的“K距离”。
所有点的K距离形成一个集合D。对D进行升序排序，依此可以形成一个样本数据的K距离图。
图中急剧变化处的值，即为Eps。
根据Eps和MinPts，计算出所有的核心点。
给核心点到小于Eps的另一个核心点赋予一个连线，到核心点的距离等于Eps的点被识别为边界点。最后，核心点、边界点之外的点都是噪声点。
将能够连线的点和与之关联的边界点都放到一起，形成了一个簇。

几种聚类的优缺点

层次聚类的优缺点：

优点：

距离和规则的相似度容易定义，限制少；
不需要预先指定聚类数；
可以发现类的层次关系；
可以聚类成其他形状。

缺点：

计算复杂度太高；
奇异值也能产生很大影响；
算法很可能聚类成链状。

DBSCAN的优缺点：

优点：

不需要事先知道要形成的簇的数量。
可以发现任意形状的簇类。
对噪声点不敏感。
对样本点的顺序不敏感。

缺点：

簇的密度变化太大时，DBSCAN会有麻烦。
对于高维数据，密度定义困难，DBSCAN也有问题。

注意：

K均值对于圆形区域聚类的效果很好，DBSCAN基于密度，对于集中区域效果很好。
对于不规则形状，K均值完全无法使用。DBSCAN可以起到很好的效果。

K均值的优缺点：

优点：

简单，易于理解和实现。
时间复杂度低。

缺点：

要手工输入K值，对初始值的设置很敏感。
对噪声和离群点很敏感。
只用于数值型数据，不适用于categorical类型的数据。
不能解决非凸数据。
主要发现圆形或者球形簇，不能识别非球形的簇。